
 9、如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′可以绕点O自由转动,就做成了一个测量工件,则A′B′的长等于内槽宽AB,则判定△OAB≌△OA′B′的理由是( )
9、如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′可以绕点O自由转动,就做成了一个测量工件,则A′B′的长等于内槽宽AB,则判定△OAB≌△OA′B′的理由是( )科目:初中数学 来源: 题型:
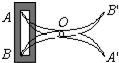 4、如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′可以绕着点O自由转动,就做成了一个测量工件,由三角形全等得出A′B′的长等于内槽宽AB;那么判定△OAB≌△OA′B′的理由是( )
4、如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′可以绕着点O自由转动,就做成了一个测量工件,由三角形全等得出A′B′的长等于内槽宽AB;那么判定△OAB≌△OA′B′的理由是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,将两根钢条AA′、BB′的中点 O连在一起,使AA′、BB′能绕着点O自由转动,就做成了一个测量工具,由三角形全等可知A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是( )
如图,将两根钢条AA′、BB′的中点 O连在一起,使AA′、BB′能绕着点O自由转动,就做成了一个测量工具,由三角形全等可知A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是( )查看答案和解析>>
科目:初中数学 来源:2014届浙江富阳环山中学七年级下学期期中考试数学试卷(解析版) 题型:填空题
如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′可以绕着点O自由转动,就做成了一个测量工件,由三角形全等得出 A′B′的长等于内槽宽AB;那么判定△OAB≌△OA′B′的理由是 ▲ 。

查看答案和解析>>
科目:初中数学 来源:2013届广西省北海市合浦县八年级上学期期末考试数学卷 题型:选择题
如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′可以绕着点O自由转动,就做成了一个测量工件,则A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是 ( )

A.边角边 B.角边角 C.边边边 D.角角边
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com