
分析 首先化简(a2-4)÷$\frac{a}{a-2}•\frac{1}{{a}^{2}-4a+4}$,然后把a=$\sqrt{2}$-1代入化简后的算式,求出算式的值是多少即可.
解答 解:(a2-4)÷$\frac{a}{a-2}•\frac{1}{{a}^{2}-4a+4}$
=$\frac{a+2}{a}$•(a-2)2•$\frac{1}{{(a-2)}^{2}}$
=$\frac{a+2}{a}$
=1+$\frac{2}{a}$
当a=$\sqrt{2}$-1时,
原式=1+$\frac{2}{\sqrt{2}-1}$=1+2$\sqrt{2}$+2=3+2$\sqrt{2}$.
点评 此题主要考查了分式的化简求值问题,要熟练掌握,注意先把分式化简后,再把分式中未知数对应的值代入求出分式的值.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{2017}{2018}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
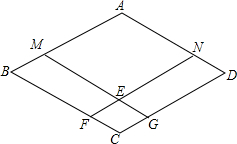 如图,已知四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E,求证:四边形AMEN是菱形.
如图,已知四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E,求证:四边形AMEN是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
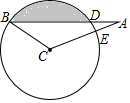 如图,在∠ABC中,∠ACB=130°,∠BAC=20°,BC=4,以点C为圆心,CB长为半径的圆交AB于点D,交AC于点E.
如图,在∠ABC中,∠ACB=130°,∠BAC=20°,BC=4,以点C为圆心,CB长为半径的圆交AB于点D,交AC于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com