
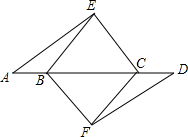
 如图,AE∥DF,CE∥BF,AB=CD,求证:BE∥CF.
如图,AE∥DF,CE∥BF,AB=CD,求证:BE∥CF. 分析 由AE∥DF,CE∥BF,可知∠A=∠D,∠DBF=∠ACE,由AB=CD,可知AC=DB,根据ASA可证△ACE≌△DBF,则BF=CE,于是四边形BFCE是平行四边形,故BE∥CF.
解答 证明:∵AE∥DF,CE∥BF,
∴∠A=∠D,∠DBF=∠ACE,
∵AB=CD,
∴AC=DB,
在△ACE和△DBF中,
$\left\{\begin{array}{l}{∠A=∠D}\\{AC=DB}\\{∠DBF=∠ACE}\end{array}\right.$,
∴△ACE≌△DBF,
∴BF=CE,
∴四边形BFCE是平行四边形,
∴BE∥CF.
点评 本题主要考查了全等三角形的判定与性质以及平行四边形的判定与性质,证明△ACE≌△DBF是解决问题的关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:解答题
 如图,某宾馆重新装修后,准备在大厅的主梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图所示(单位:米),求购买地毯至少需要多少元.
如图,某宾馆重新装修后,准备在大厅的主梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图所示(单位:米),求购买地毯至少需要多少元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,l4和l1,l2相交于C,D两点,点P在直线AB上,
如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,l4和l1,l2相交于C,D两点,点P在直线AB上,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com