
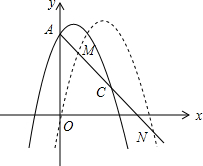 如图,已知抛物线y=-x2+3x+6交y轴于A点,点C(4,k)在抛物线上,将抛物线向右平移n个单位长度后与直线AC交于点M、N两点,且M、N关于点C成中心对称,求n的值.
如图,已知抛物线y=-x2+3x+6交y轴于A点,点C(4,k)在抛物线上,将抛物线向右平移n个单位长度后与直线AC交于点M、N两点,且M、N关于点C成中心对称,求n的值. 分析 根据自变量与函数值的对应关系,可得A、C点坐标,根据待定系数法,可得AC的解析式,根据图象向右平移减,可得平移后的解析式,根据解方程组,可得关于x的方程,根据根与系数的关系,可得两根之和,根据中点坐标公式,可得关于n的方程,根据解方程,可得答案.
解答 解:设M(x1,y1),N(x2,y2),
当x=0时,y=6,即A(0,6),
当x=4时,k=y=-42+3×4+6=2,即C(4,2),
AC的解析式为y=kx+b,将A、C点坐标代入,得
$\left\{\begin{array}{l}{b=6}\\{4k+b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=6}\end{array}\right.$.
故AC的解析式为y=-x+6,
设平移后的解析式为y=-(x-n)2+3(x-n)+6=-x2+(2n+3)x-n2-3n+6,
联立AC与新抛物线,得$\left\{\begin{array}{l}{y=-x+6}\\{y=-{x}^{2}+(2n+3)x-{n}^{2-3n+6}}\end{array}\right.$,
-x2+(2n+4)x-n2-3n=0
x1+x2=2n+4,
C点的横坐标$\frac{{x}_{1}+{x}_{2}}{2}$=n+2=4,
解得n=2.
点评 本题考查了二次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减,注意两根之和等于-$\frac{b}{a}$,又利用了中点坐标公式:M(x1,y1),N(x2,y2),中点的坐标($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$).


科目:初中数学 来源: 题型:解答题
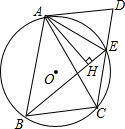 如图,已知四边形ABCD是平行四边形,边CD与⊙O相交于点E,连接AE,BE,∠DAE=∠ABE
如图,已知四边形ABCD是平行四边形,边CD与⊙O相交于点E,连接AE,BE,∠DAE=∠ABE查看答案和解析>>
科目:初中数学 来源: 题型:解答题
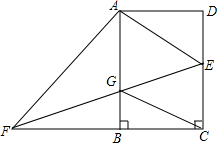 如图,在矩形ABCD中,AB=4,BC=2,点E是边CD上任意一点(点E与点C、D不重合),过点A作AF⊥AE,交边CB的延长线于点F,连接EF交边AB于点G.
如图,在矩形ABCD中,AB=4,BC=2,点E是边CD上任意一点(点E与点C、D不重合),过点A作AF⊥AE,交边CB的延长线于点F,连接EF交边AB于点G.查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省长宁县双河学区八年级下学期第一次联考数学试卷(解析版) 题型:解答题
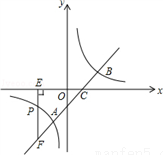
(9分)如图,直线y=x﹣1与反比例函数y=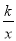 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
(1)求反比例函数的解析式;
(2)若点P(n,﹣1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省长宁县双河学区八年级下学期第一次联考数学试卷(解析版) 题型:填空题
直线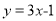 向右平移2个单位得到的直线的解析式为:____________
向右平移2个单位得到的直线的解析式为:____________
查看答案和解析>>
科目:初中数学 来源:2017届四川省遂宁市九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,二次函数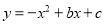 的图象经过坐标原点,与
的图象经过坐标原点,与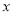 轴的另一个交点为A(-2,0).
轴的另一个交点为A(-2,0).

(1)求二次函数的解析式
(2)在抛物线上是否存在一点P,使△AOP的面积为3,若存在请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com