
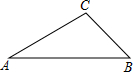
 已知:△ABC,AB=4,AC=3,以CB为边作等边三角形△CBP,连接AP,求AP的值.
已知:△ABC,AB=4,AC=3,以CB为边作等边三角形△CBP,连接AP,求AP的值.分析 (1)根据题意画出图形即可;
(2)△ACP以P点为旋转中心,逆时针旋转60°,得到△P′BP,只要证明△ABP′是直角三角形,利用勾股定理即可解决问题;
(3)当∠CAB=120°,最大值是7.证明方法类似(2).
解答 解:(1)补全图形如图所示,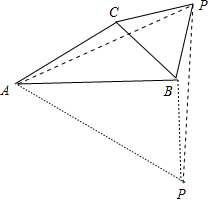
(2)∵△ACP以P点为旋转中心,逆时针旋转60°,得到△P′BP
∴△ACP≌△P′BP
∴∠ACP=∠P′BP,AP=P′P,∠CPA=∠P′PB,
AC=P′B=3,
∵△CBP为等边三角形
∴∠APP′=60°∠CBP=60°,
∴△P′AP为等边三角形
∴AP=AP′,
∵∠CAB=30°,
∴∠ACB+∠ABC=150°
∴∠ABP′=360°-150°-120°=90°
在Rt△ABP′中
AP=AP′=$\sqrt{{4^2}+{3^2}}$=5,
(3)结论:当∠CAB=120°,最大值是7.
图形:如图所示,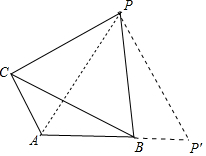
思路:
①由∠CAB=120°,可得∠ACB+∠ABC=60°,
②由(2)中的旋转后的全等,可得∠ACP=∠P′BP,AP=P′P,AC=P′B,
③由∠CBP=60°,进而推出∠ABC+∠CBP+∠P′BP=180°(即点A、B、P共线),
④由AC=3,AB=4,可得AP=AP′=AB+BP′=7.
点评 本题考查几何变换综合题、等边三角形的性质、旋转变换、勾股定理等知识,解题的关键是学会用旋转法添加辅助线构造全等三角形解决问题,属于中考压轴题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
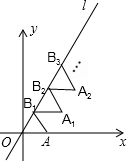 如图,等边三角形△OAB1的一边OA在x轴上,且OA=1,当△OAB1沿直线l滚动,使一边与直线l重合得到△B1A1B2,△B2A2B3,…则点A2017的坐标是($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$).
如图,等边三角形△OAB1的一边OA在x轴上,且OA=1,当△OAB1沿直线l滚动,使一边与直线l重合得到△B1A1B2,△B2A2B3,…则点A2017的坐标是($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+2)(x-2)-3x | B. | x(x-3)-4 | C. | (x-1)(x+4) | D. | (x+1)(x-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
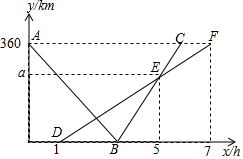 快、慢两车分别从相距360km的佳市、哈市两地出发,匀速行驶,先相向而行,慢车在快车出发1h后出发,到达佳市后停止行驶,快车到达哈市后,立即按原路原速返回佳市(快车调头的时间忽略不计),快、慢两车距哈市的路程y1(单位:km),y2(单位:km)与快车出发时间x(单位:h)之间的函数图象如图所示,请结合图象信息解答下列问题:
快、慢两车分别从相距360km的佳市、哈市两地出发,匀速行驶,先相向而行,慢车在快车出发1h后出发,到达佳市后停止行驶,快车到达哈市后,立即按原路原速返回佳市(快车调头的时间忽略不计),快、慢两车距哈市的路程y1(单位:km),y2(单位:km)与快车出发时间x(单位:h)之间的函数图象如图所示,请结合图象信息解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com