
【题目】如果一元二次方程ax2+bx+c=0 的两根 x1,x2均为正数,其中x1>x2,且满足1<x1﹣x2<2,那么称这个方程有“友好根”.
(1)方程(x﹣![]() )(x﹣
)(x﹣![]() )=0_____“友好根”(填:“有”或“没有”);
)=0_____“友好根”(填:“有”或“没有”);
(2)已知关于x的 x2﹣(t﹣1)x+t﹣2=0有“友好根”,求 t的取值范围.
【答案】(1)没有;(2)4<t<5.
【解析】
(1)先解方程得到x1![]() ,x2
,x2![]() ,则不满足1<x1﹣x2<2,所以可判断方程没有“友好根”;
,则不满足1<x1﹣x2<2,所以可判断方程没有“友好根”;
(2)根据判别式的意义得到△=(t﹣1)2﹣4×1×(t﹣2)=(t﹣3)2>0,利用求根公式解得x1=t﹣2,x2=1或x1=t﹣2,x2=1,然后讨论:若x1=t﹣2,x2=1,则得到4<t<5;若x1=1,x2=t﹣2,则不合题意,最后综合得到t的取值范围.
(1)方程(x![]() )(x
)(x![]() )=0 没有“友好根”,理由如下:
)=0 没有“友好根”,理由如下:
∵(x![]() )(x
)(x![]() )=0,∴x1
)=0,∴x1![]() ,x2
,x2![]() ,这时x1>0,x2>0,但x1﹣x2<1,∴不满足x1>x2且满足1<x1﹣x2<2这个条件,∴方程(x
,这时x1>0,x2>0,但x1﹣x2<1,∴不满足x1>x2且满足1<x1﹣x2<2这个条件,∴方程(x![]() )(x
)(x![]() )=0 没有“友好根”.
)=0 没有“友好根”.
故答案为:没有;
(2)x2﹣(t﹣1)x+t﹣2=0,由已知△=(t﹣1)2﹣4×1×(t﹣2)=(t﹣3)2>0,∴x![]() ,∴当t>3时,x1=t﹣2,x2=1,当t<3时,x1=1,x2=t﹣2.
,∴当t>3时,x1=t﹣2,x2=1,当t<3时,x1=1,x2=t﹣2.
∵一元二次方程ax2+bx+c=0有“友好根”,∴x1,x2均为正数,x1>x2且满足1<x1﹣x2<2,若x1=t﹣2,x2=1,则1<t﹣2﹣1<2,解得:4<t<5;
若x1=1,x2=t﹣2,则![]() ,无解.
,无解.
综上,t的取值范围是4<t<5.


科目:初中数学 来源: 题型:
【题目】(9分)如图,在平面直角坐标系中,点A(![]() ,1)、B(2,0)、O(0,0),反比例函数y=
,1)、B(2,0)、O(0,0),反比例函数y=![]() 图象经过点A.
图象经过点A.
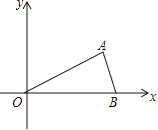
(1)求k的值;
(2)将△AOB绕点O逆时针旋转60°,得到△COD,其中点A与点C对应,试判断点D是否在该反比例函数的图象上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形 ABCD 中,AB=2,∠DAB=60°,点 E 是 AD 边的中点,点 M 是 AB 边上的一个动点(不与点 A 重合), 延长 ME 交 CD 的延长线于点 N,连接MD,AN.

(1)求证:四边形 AMDN 是平行四边形.
(2)当 AM 的值为何值时,四边形 AMDN 是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
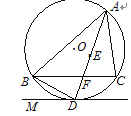
如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D;连接BD,过点D作直线DM,使∠BDM=∠DAC.
(1)求证:直线DM是⊙O的切线;
(2)求证:DE2=DF·DA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是![]() 的直径,弦AB⊥CD于点G,直线EF与
的直径,弦AB⊥CD于点G,直线EF与![]() 相切与点D,则下列结论中不一定正确的是
相切与点D,则下列结论中不一定正确的是
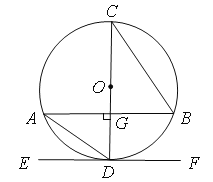
(A)AG=BG (B)AB∥EF (C)AD∥BC (D)∠ABC=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,剪两张对边平行且宽度相等的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )

A. ∠ABC=∠ADC,∠BAD=∠BCD B. AB=BC
C. AB=CD,AD=BC D. ∠DAB+∠BCD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
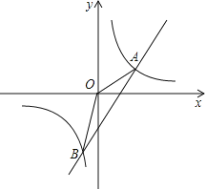
【题目】如图,一次函数![]() (
(![]() )的图象与反比例函数
)的图象与反比例函数![]() (
(![]() )的图象相交于A、B两点且点A的坐标为(2,1).
)的图象相交于A、B两点且点A的坐标为(2,1).
(1)分别求出一次函数与反比例函数的解析式以及点B的坐标;
(2)当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究问题:一个不透明的盒中装有若干个白球,怎样估算白球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验.摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
统计结果如表:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到有记号球的次数m | 25 | 44 | 57 | 105 | 160 | 199 |
摸到有记号球的频率 | 0.25 | 0.22 | 0.19 | 0.21 | 0.20 | 0.20 |
(1)请你完成上表中数据,并估计摸到有记号球的概率是多少?
(2)估计盒中共有球多少个?没有记号球有多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com