
���� ��1�����ݵ��������ε����ʺͽ�ƽ�������ʵó����ɣ�
��2��֤��OMA�ա�ONC��ASA�������ɵó��𰸣�
��3���������DMCN���ó�CM=DN����MOC�ա�NOB��SAS�����Ƴ�OM=ON����MOC=��NOB���ó���MOC+��CON=��NOB+��CON�������MON=��BOC=90�㣬���ɵó��𰸣�
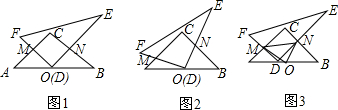
���  �⣺��1����ͼ1���ߡ�ACB=90�㣬CA=CB����FDE=90�㣬DF��AC��
�⣺��1����ͼ1���ߡ�ACB=90�㣬CA=CB����FDE=90�㣬DF��AC��
���DNC=90�㣬
��DE��BC��
����CO����CO��AB�������ߣ�
��CA=CB��
��CO�ǡ�ACB�Ľ�ƽ���ߣ�
��OM��AC��ON��BC��
��OM=ON��
��2��OM=ON��
���ɣ���ͼ2������CO����CO��AB�������ߣ�
�ߡ�ACB=90�㣬CA=CB��
��CO�ǡ�ACB�Ľ�ƽ���ߣ���BAC=45�㣬OC=$\frac{1}{2}$AB=OA��OC��AB��
���OCB=45�㣬
���OAM=��OCN=45�㣬
�ߡ�AOM+��MOC=90��=��CON+��MOC��
���AOM=��CON��
�ڡ�OMA���ONC�У�
$\left\{\begin{array}{l}{��OAM=��OCN}\\{OA=OC}\\{��AOM=��CON}\end{array}\right.$
���OMA�ա�ONC��ASA����
��OM=ON��
��3����OMN�ǵ���ֱ�������Σ�
���ɣ���ͼ3��
�ߡ�ACB=90�㣬FD��CA��ֱ�ཻ�ڵ�M��BC��DE��ֱ�ཻ�ڵ�N��
���ı���MDNC�Ǿ��Σ�
��MC=DN��
��DE��BC����B=45�㣬
���NDB=45�㣬
���NDB=��B��
��BN=DN��
��MC=BN��
����CO����CO��AB�������ߣ�
�ߡ�ACB=90�㣬CA=CB��
��CO�ǡ�ACB�Ľ�ƽ���ߣ���BAC=45�㣬OC=$\frac{1}{2}$AB=OB��OC��AB��
���OCA=45�㣬
���OCA=��B=45�㣬
�ڡ�OMC���ONB�У�
$\left\{\begin{array}{l}{CM=BN}\\{��OCM=��B}\\{OC=OB}\end{array}\right.$
���OMC�ա�ONB��SAS����
��OM=ON����COM=��BON��
�ߡ�CON+��BON=90�㣬
���COM+��CON=90�㣬
����MON=90�㣬
��OM��ON��
���OMN�ǵ���ֱ�������Σ�
���� ���⿼���˵��������ε����ʺ��ж���ȫ�������ε����ʺ��ж������ε����ʺ��ж�����ƽ�������ʵ�֪ʶ���Ӧ�ã���Ҫ����ѧ�����ö���������������������Ŀ�ȽϺã��ۺ���Ҳ�Ƚ�ǿ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��н/��Ԫ | 25 | 15 | 10 | 6 | 4 |
| ���� | 1 | 1 | 3 | 3 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com