如图，阳光下，小亮的身高如图中线段AB所示，他在地面上的影子如图中线段BC所示，线段DE表示旗杆的高，线段FG表示一堵高墙．
（1）请你在图中画出旗杆在同一时刻阳光照射下形成的影子；
（2）如果小亮的身高AB=1.6m，他的影子BC=2.4m，旗杆的高DE=15m，旗杆与高墙的距离EG=16m，请求出旗杆的影子落在墙上的长度．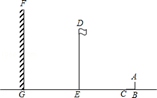
科目：初中数学 来源： 题型：计算题
如图D，E分别是△ABC的AB，AC边上的点，且DE∥BC，AD∶AB=1∶4，
（1）证明：△ADE∽△ABC；
（2）当DE=2，求BC的长.
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，在△PAB中，点C、D在边AB上，PC＝PD＝CD，∠APB＝120°．
(1)试说明△APC与△PBD相似．
(2)若CD＝1，AC＝x，BD＝y，请你求出y与x之间的函数关系式．
(3)小明猜想：若PC＝PD＝1，∠CPD＝α，∠APB＝β，只要α与β之间满足某种关系式，问题(2)中的函数关系式仍然成立．你同意小明的观点吗？如果你同意，请求出α与β所满足的关系式；若不同意，请说明理曲．
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，⊙O的直径CD垂直于弦AB，垂足为E，F为DC延长线上一点，且∠CBF=∠CDB．
（1）求证：FB为⊙O的切线；
（2）若AB=8，CE=2，求sin∠F．
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，在△ABC中，D是BC边上的点（不与点B、C重合），连结AD．
问题引入：
（1）如图①，当点D是BC边上的中点时，S△ABD：S△ABC= ；当点D是BC边上任意一点时，S△ABD：S△ABC= （用图中已有线段表示）．
探索研究：
（2）如图②，在△ABC中，O点是线段AD上一点（不与点A、D重合），连结BO、CO，试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比，并说明理由．
拓展应用：
（3）如图③，O是线段AD上一点（不与点A、D重合），连结BO并延长交AC于点F，连结CO并延长交AB于点E，试猜想
的值，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图①，将一张矩形纸片对折，然后沿虚线剪切，得到两个（不等边）三角形纸片△ABC，△A1B1C1．
（1）将△ABC，△A1B1C1如图②摆放，使点A1与B重合，点B1在AC边的延长线上，连接CC1交BB1于点E．
①求证：四边形C1B1AB为梯形.
②若∠A="45°," ∠ABC="30°," 求∠B1C1C的度数
（2）若将△ABC，△A1B1C1如图③摆放，使点B1与B重合，点A1在AC边的延长线上，连接CC1交A1B于点F．试判断∠A1C1C与∠A1BC是否相等，并说明理由．
（3）在（2）的条件下，若AC＝3，B1C1＝6，设A1B＝x，C1F＝y，写出y与x的函数关系式（不要求写出自变量的取值范围）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
米．
中，点
、
分别在边
、
上，
平分
，
，如果
，
，那么
．
中，
∥
，点
在
上，连接
并延长与
．
∽△
； 
∥
于点
，若
，求