
分析 (1)A城运往C乡的农机为x台,则可得A城运往D乡的农机为30-x台,B城运往C乡的农机为34-x台,B城运往D乡的农机为40-(34-x)台,从而可得出W与x的函数关系.
(2)根据题意得140x+12540≥16460求得28≤x≤30,于是得到有3种不同的调运方案,写出方案即可;
(3)根据题意得到W=(140-a)x+12540,y=-60x+12540,于是得到当x=30时,总费用最少.
解答 解:(1)W=250x+200(30-x)+150(34-x)+240(6+x)=140x+12540(0≤x≤30);
(2)根据题意得140x+12540≥16460,
∴x≥28,
∵x≤30,
∴28≤x≤30,
∴有3种不同的调运方案,
第一种调运方案:从A城调往C城28台,调往D城2台,从B城调往C城6台,调往D城34台;
第二种调运方案:从A城调往C城29台,调往D城1台,从B城调往C城5台,调往D城35台;
第三种调运方案:从A城调往C城30台,调往D城0台,从B城调往C城4台,调往D城36台,
(3)W=(250-a)x+200(30-x)+150(34-x)+240(6+x)=(140-a)x+12540,
①当0<a<140时,即:140-a>0,
当x=0时,W最小值=12540元,
此时从A城调往C城0台,调往D城30台,从B城调往C城34台,调往D城6台;
②当a=140时,W=12540元,
∴各种方案费用一样多;
③当140<a≤200时,140-a<0,
∴当a=200时,W=-60x+12540,
当x=30时,W最小值=10740元,
此时从A城调往C城30台,调往D城0台,从B城调往C城4台,调往D城36台.
点评 本题考查一次函数的应用,属于一般的应用题,解答本题的关键是根据题意得出y与x的函数关系式,另外同学们要掌握运用函数的增减性来判断函数的最值问题.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P=40°,则∠ABC的度数为( )
如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P=40°,则∠ABC的度数为( )| A. | 20° | B. | 25° | C. | 40° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
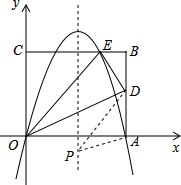 如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.
如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com