
分析 (1)依题意当销售单价定为x元时,年销售量减少$\frac{1}{10}$(x-100),则易求y与x之间的函数关系式,进而由题意易得Z与x之间的函数关系.
(2)把z与x的关系式化简,得出当x=170时,z取最大值;即可得出公司是盈利了还是亏损;
(3)根据z=(30-$\frac{1}{10}$x)(x-40)-310=-$\frac{1}{10}$x2+34x-1510=1130进而得出当120≤x≤220时,z≥1130画出图象得出即可.
解答 解:(1)依题意知,当销售单价定为x元时,年销售量减少$\frac{1}{10}$(x-100)万件,
∴y=20-$\frac{1}{10}$(x-100)=-$\frac{1}{10}$x+30,
即y与x之间的函数关系式是y=-$\frac{1}{10}$x+30.
由题意得:
z=y(x-40)-2000
=(30-$\frac{1}{10}$x)(x-40)-2000
=-$\frac{1}{10}$x2+34x-3200,
即z与x之间的函数关系是z=-$\frac{1}{10}$x2+34x-3200.
(2)∵z=-$\frac{1}{10}$x2+34x-3200,
=-$\frac{1}{10}$(x-170)2-310.
∴当x=170时,z取最大值,为-310,
即当销售单价为170元,年获利最大,并且第一年年底公司还差310万元就可收回全部投资.
(3)第二年的销售单价定为x元时,年获利为:
z=(30-$\frac{1}{10}$x)(x-40)-310=-$\frac{1}{10}$x2+34x-1510.
当z=1130时,即1130=-$\frac{1}{10}$x2+34x-1510,
整理得x2-340x+26400=0,
解得:x1=120,x2=220.
函数z=-$\frac{1}{10}$x2+34x-1510的图象大致如图所示,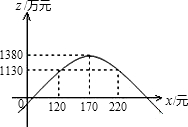
由图象可以看出:当120≤x≤220时,z≥1130.
故第二年的销售单价应确定在不低于120元且不高于220元的范围内.
点评 本题主要考查了二次函数的应用和一元二次方程的解法以及二次函数图象等知识,根据已知得出z与x之间的函数关系是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
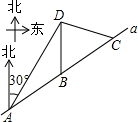 如图,我市云台山景区内一条笔直的公路a经过三个景点A、B、C,现在市政府决定开发风景优美的景点D.经测量景点D位于景点A的北偏东30°方向12km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上.已知AB=4$\sqrt{3}$km.
如图,我市云台山景区内一条笔直的公路a经过三个景点A、B、C,现在市政府决定开发风景优美的景点D.经测量景点D位于景点A的北偏东30°方向12km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上.已知AB=4$\sqrt{3}$km.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
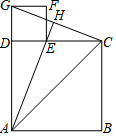 如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A、D、G在同一直线上,且AD=3,DE=1,连接AC、CG、AE,并延长AE交OG于点H.
如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A、D、G在同一直线上,且AD=3,DE=1,连接AC、CG、AE,并延长AE交OG于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 材料1:
材料1:| 恩格尔系数 大于或等于60% | 恩格尔系数 在50%~60%之间 | 恩格尔系数 在40%~50%之间 | 恩格尔系数 在30%~40%之间 | 恩格尔系数 小于30% |
| 绝对贫困 | 温 饱 | 小 康 | 富 裕 | 最富裕 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com