
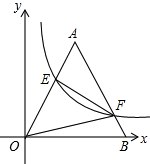
 若双曲线y=$\frac{k}{x}$与边长为4的等边△AOB的边OA,AB分别相交于E,F两点,且EF⊥AE,则实数k的值为$\frac{36\sqrt{3}}{25}$.
若双曲线y=$\frac{k}{x}$与边长为4的等边△AOB的边OA,AB分别相交于E,F两点,且EF⊥AE,则实数k的值为$\frac{36\sqrt{3}}{25}$. 分析 过E点作EH⊥OB于点H,过F点作FC⊥OB于点C,设FB=x,利用等边三角形的性质及锐角三角函数定义表示出FC与BC,进而表示出AF与OC,表示出AE与OE的长,得出OE与EH的长,表示出E与F坐标,根据E与F都在反比例函数的图象上,得到横纵坐标乘积相等列出方程,求出方程的解得到x的值,即可求出实数k的值.
解答  解:过E点作EH⊥OB于点H,过F点作FC⊥OB于点C,设BF=x.
解:过E点作EH⊥OB于点H,过F点作FC⊥OB于点C,设BF=x.
∵△AOB是边长为4的等边三角形,
∴AB=OA=OB=4,∠AOB=∠ABO=∠A=60°,
∴BC=FB•cos∠FBC=$\frac{1}{2}$x,FC=FB•sin∠FBC=$\frac{\sqrt{3}}{2}$x,
∴AF=4-x,OC=OB-BC=4-$\frac{1}{2}$x,
∵EF⊥AE,
∴AE=AF•cosA=2-$\frac{1}{2}$x,
∴OE=OA-AE=$\frac{1}{2}$x+2,
∴OH=OE•cos∠AOB=$\frac{1}{4}$x+1,EH=OE•sin∠AOB=$\frac{\sqrt{3}}{4}$x+$\sqrt{3}$,
∴E($\frac{1}{4}$x+1,$\frac{\sqrt{3}}{4}$x+$\sqrt{3}$),F(4-$\frac{1}{2}$x,$\frac{\sqrt{3}}{2}$x),
∵E、F都在双曲线y=$\frac{k}{x}$的图象上,
∴k=($\frac{1}{4}$x+1)($\frac{\sqrt{3}}{4}$x+$\sqrt{3}$)=(4-$\frac{1}{2}$x)•$\frac{\sqrt{3}}{2}$x,
解得:x1=4,x2=$\frac{4}{5}$,
当x1=4时,BF=4,AF=0,不合题意舍去,
∴x=$\frac{4}{5}$,
∴k=(4-$\frac{1}{2}$×$\frac{4}{5}$)•$\frac{\sqrt{3}}{2}$×$\frac{4}{5}$=$\frac{36\sqrt{3}}{25}$.
故答案为$\frac{36\sqrt{3}}{25}$.
点评 本题考查了反比例函数与一次函数的交点问题,等边三角形的性质,解直角三角形,反比例函数图象上点的坐标特征,设FB=x,用含x的代数式表示出E与F点的坐标是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息解答下列问题.
一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种板材(m2/套) | 乙种板材(m2/套) | 获利(元/套) | |
| A款 | 3 | 7 | 600 |
| B款 | 5 | 3 | 400 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=3cm,⊙O是以BC为直径的圆,如果⊙O与⊙S相内切,那么⊙A的半径为$\sqrt{13}+2$cm.
如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=3cm,⊙O是以BC为直径的圆,如果⊙O与⊙S相内切,那么⊙A的半径为$\sqrt{13}+2$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com