
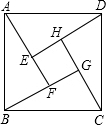
 如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为( )
如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{{2\sqrt{13}}}{13}$ |
分析 小正方形EFGH面积是a2,则大正方形ABCD的面积是13a2,则小正方形EFGH边长是a,则大正方形ABCD的边长是$\sqrt{13}$a,设AE=DH=x,利用勾股定理求出x,最后利用熟记函数即可解答.
解答 解:设小正方形EFGH面积是a2,则大正方形ABCD的面积是13a2,
∴小正方形EFGH边长是a,则大正方形ABCD的边长是$\sqrt{13}$a,
∵图中的四个直角三角形是全等的,
∴AE=DH,
设AE=DH=x,
在Rt△AED中,AD2=AE2+DE2,
即13a2=x2+(x+a)2
解得:x1=2a,x2=-3a(舍去),
∴AE=2a,DE=3a,
∴tan∠ADE=$\frac{AE}{DE}$=$\frac{2}{3}$,
故选:C.
点评 此题中根据正方形以及直角三角形的面积公式求得直角三角形的三边,进一步运用锐角三角函数的定义求解.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{x(x-1)}{2}$=2550 | B. | $\frac{x(x+1)}{2}$=2550 | C. | x(x-1)=2550 | D. | x(x+1)=2550 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对某区中小学生的睡眠时间的调查 | |
| B. | 对我市初中学生的兴趣爱好的调查 | |
| C. | 对我市中学教师的健康状况的调查 | |
| D. | 对“天宫二号”飞行器各零部件的质量的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点E坐标为(0,-$\sqrt{3}$),点P是对角线OC上一个动点,则EP+BP最短的最短距离为$\sqrt{13}$.
菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点E坐标为(0,-$\sqrt{3}$),点P是对角线OC上一个动点,则EP+BP最短的最短距离为$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在“校园读书月”活动中,小华调查了班级里40名同学本学期购买课外书的花费情况,并将结果绘制成如图所示的统计图.下面有四个推断:
在“校园读书月”活动中,小华调查了班级里40名同学本学期购买课外书的花费情况,并将结果绘制成如图所示的统计图.下面有四个推断:| A. | ①② | B. | ?②④ | C. | ①③ | D. | ?①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有解,x=1 | B. | 有解,x=5 | C. | 有解,x=4 | D. | 无解 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com