
 ��ͼ����ֱ֪��y=
��ͼ����ֱ֪��y= ����������A��B ���㣬���߶�ABΪ��������������ABCD������A��D��C����������ֱ����һ������ΪE��
����������A��B ���㣬���߶�ABΪ��������������ABCD������A��D��C����������ֱ����һ������ΪE�� ����λ���ȵ��ٶ�������AB�»���ֱ������D����x����ʱֹͣ��������������x���·����ֵ����ΪS����S���ڻ���ʱ��t�ĺ�����ϵʽ����д����Ӧ�Ա���t��ȡֵ��Χ��
����λ���ȵ��ٶ�������AB�»���ֱ������D����x����ʱֹͣ��������������x���·����ֵ����ΪS����S���ڻ���ʱ��t�ĺ�����ϵʽ����д����Ӧ�Ա���t��ȡֵ��Χ�� ��ֱ��y=
��ֱ��y= ��
��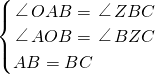 ��
�� ��
��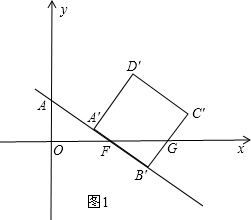 ��ã�a=-
��ã�a=- ��b=
��b=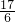 ��c=1��
��c=1�� x2+
x2+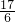 x+1��
x+1�� ��
�� =
= ��
�� =
= =
= ��
��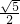 t��
t�� ��S��FB��G=
��S��FB��G= FB���GB��=
FB���GB��= •
• t•
t•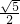 t��
t�� t2��
t2�� ��
�� t-
t- ��
�� ��
��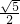 t��
t�� ��A��G+B��H��•A��B��=
��A��G+B��H��•A��B��= •��
•�� +
+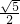 t��
t��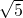 ��
�� t-
t- ��
�� ��2��t��3ʱ����ͼ3��
��2��t��3ʱ����ͼ3�� ��
�� -
- =
=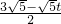 ��
�� ��2��1=1��OA=1����AOF=��FA��G=90�㣬��AFO=��GFA�䣬
��2��1=1��OA=1����AOF=��FA��G=90�㣬��AFO=��GFA�䣬 =��
=�� ��2��
��2��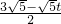 ��2��
��2�� ��2-��
��2-��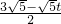 ��2��
��2�� t2+
t2+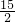 t-
t-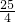 ��
��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 2x |
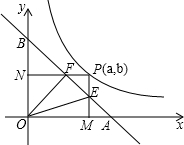 ��һ���ڵĵ����P��PM��x����M��PN��y����N����������ֱ��AB����E��F��
��һ���ڵĵ����P��PM��x����M��PN��y����N����������ֱ��AB����E��F��| 1 |
| 2x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
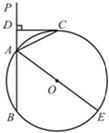 23����ͼ����ֱ֪��PA����O��A��B���㣬AE�ǡ�O��ֱ������CΪ��O��һ�㣬��ACƽ�֡�PAE����C��CD�APA������ΪD��
23����ͼ����ֱ֪��PA����O��A��B���㣬AE�ǡ�O��ֱ������CΪ��O��һ�㣬��ACƽ�֡�PAE����C��CD�APA������ΪD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
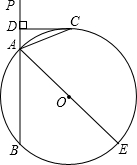 ��2012•��ƽ��һģ����ͼ����ֱ֪��PA����O��A��B���㣬AE�ǡ�O��ֱ����CΪ��O��һ�㣬��ACƽ�֡�PAE������C��CD��PA��D��
��2012•��ƽ��һģ����ͼ����ֱ֪��PA����O��A��B���㣬AE�ǡ�O��ֱ����CΪ��O��һ�㣬��ACƽ�֡�PAE������C��CD��PA��D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����ֱ֪��MA����O��A��B���㣬BC�ǡ�O��ֱ������D�ڡ�O�ϣ���BDƽ�֡�MBC����D��DE��MA������ΪE��
��ͼ����ֱ֪��MA����O��A��B���㣬BC�ǡ�O��ֱ������D�ڡ�O�ϣ���BDƽ�֡�MBC����D��DE��MA������ΪE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
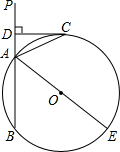 ��ͼ����ֱ֪��PA����O��A��B���㣬AE�ǡ�O��ֱ������CΪ��O��һ�㣬��ACƽ�֡�PAE����C��CD��PA������ΪD��
��ͼ����ֱ֪��PA����O��A��B���㣬AE�ǡ�O��ֱ������CΪ��O��һ�㣬��ACƽ�֡�PAE����C��CD��PA������ΪD���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com