
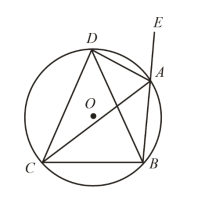
【题目】如图,AD 是△ABC 外角∠EAC 的平分线,AD 与△ABC 的外接圆⊙O 交于点 D.
(1)求证:DB=DC;
(2)若∠CAB=30°,BC=4,求劣弧 CD 的长度.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由DA平分∠EAC可得∠EAD=∠DAC,可证的∠EAD=∠DCB,∠DCB=∠DBC
可得DC=BC;
(2) 可证△COB为等边三角形,可得OC=BC=4,∠DBC=∠DCB,∠DCB=∠DBC=75°可得∠DOC的度数,可得劣弧 CD 的长度.
(1)∵DA平分∠EAC,
∴∠EAD=∠DAC
∵∠EAD+∠DAB=180°
∠DAB+∠DCB=180°
∴∠EAD=∠DCB
又∵∠DAC=∠DBC
∠DCB=∠DBC
∴DC=BC
(2)∠CDB=∠CAB=30°
∠COB=2∠CDB=60°
∴△COB为等边三角形
∴OC=BC=4
∵DC=DB
∴∠DBC=∠DCB
又∵∠DBC+∠DCB+∠CDB=180°
∴∠DCB=∠DBC=75°
∴∠DOC=2∠DBC=150°
![]()


科目:初中数学 来源: 题型:
【题目】两个反比例函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y=![]() 的图象上,PC⊥x轴于点C,交y=
的图象上,PC⊥x轴于点C,交y=![]() 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y=![]() 的图象于点B,当点P在y=
的图象于点B,当点P在y=![]() 的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②四边形PAOB的面积不会发生变化;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②四边形PAOB的面积不会发生变化;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
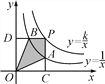
A. ①②③ B. ②③④ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的一个顶点与坐标原点重合,OC、OA分别在x轴和y轴上,正方形CDEF的一条边在x轴上,另一条边CF在BC上,反比例函数y=![]() 的图象经过B、E两点,已知OA=2,则正方形的边长是( )
的图象经过B、E两点,已知OA=2,则正方形的边长是( )
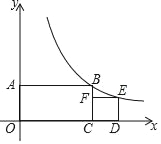
A. 2![]() -2 B.
-2 B. ![]() C. 4
C. 4![]() -2 D. 4﹣2
-2 D. 4﹣2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列说法不正确的是( )
(k≠0),下列说法不正确的是( )
A. 它的图象分布在第一、三象限 B. 点(k,k)在它的图象上
C. 它的图象关于原点对称 D. 在每个象限内y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
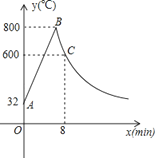
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,过点A作直线EF.
(1)如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三种情况).
(ī) (īī) (īīī)
(2)如图(2),若AB为非直径的弦,∠CAE=∠B,则EF是⊙O的切线吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
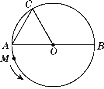
【题目】如图,在⊙O中,AB为⊙O的直径,AC是弦,OC=4,∠OAC=60°.
(1)求∠AOC的度数;
(2)如图,一动点M从A点出发,在⊙O上按逆时针方向运动,当S△MAO=S△CAO时,求动点M所经过的弧长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数的图象过点(1,﹣2).
(1)求此正比例函数的解析式;
(2)若一次函数图象是由(1)中的正比例函数的图象平移得到的,且经过点(1,2),求此一次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com