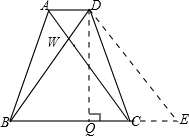过D作DE∥AC交BC的延长线于E,DQ⊥BC于Q,证四边形ADEC是平行四边形,可推出AD=CE,DE=AC,根据等腰梯形性质可以得到AC=BD=DE,再证△DBE是等边三角形,可以求出QE,再根据直角三角形性质求出DE,根据勾股定理求出DQ即可.
解:
过D作DE∥AC交BC的延长线于E,DQ⊥BC于Q,
(1)当∠BWC=60°时,
当∵AD∥BC,DE∥AC,
∴四边形ADEC是平行四边形,
∴AC=DE,∠BDE=∠BWC=60°,AD=CE,
∴BE=2

∵AD∥BC,AB=CD,
∴AC=BD=DE,
∴三角形DBE是等边三角形,
∴∠E=60°,
∵DQ⊥BC,
∴BQ=QE=

×2

=

,
∵∠QDE=90°﹣60°=30,
∴DE=2EQ=2

,
在△DQE中,由勾股定理得:DQ=

=3,
(2)当∠DWC=60°时,
∠BWC=180°﹣60°=120°,
又AC∥DE,
∴∠BDE=∠BWC=120°,
∴△BDE是等腰三角形,且底边BE=2

,
因而∠CED=(180°﹣120°)×

=30°,
作DQ⊥BE,则QE=

,DQ=

×tan30°=1,
故答案为:3或1.
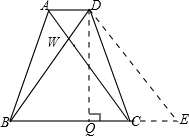


 ,则该梯形的高为 .
,则该梯形的高为 .

 ×2
×2 =
= ,
, ,
, =3,
=3, ,
, =30°,
=30°, ,DQ=
,DQ= ×tan30°=1,
×tan30°=1,