
一次函数y=(k-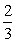 )x-3k+10(k为偶数)的图象经过第一、二、三象限,与x轴、y轴分别交于A、B两点,过点B作一直线与坐标轴围成的三角形面积为2,交x轴于点C.
)x-3k+10(k为偶数)的图象经过第一、二、三象限,与x轴、y轴分别交于A、B两点,过点B作一直线与坐标轴围成的三角形面积为2,交x轴于点C.
(1)求k的值;
(2)若一抛物线经过点A、B、C三点,求此抛物线的解析式。
(3)当抛物线开口向上时过A、B、C三点作△ABC,求tan∠ABC的值。
 解(1)⑴由题意得:
解(1)⑴由题意得: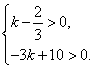 ,
,
解得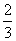 <k<
<k<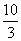 ,又k为偶数,∴k=2
,又k为偶数,∴k=2
⑵求得A(-3,0)、B(0,4),
∴OB=4,
∵S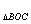 =
=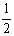 ·OB·OC==2·OC=2,
·OB·OC==2·OC=2,
∴OC=1
∴C(1,0)或(-1,0)
若取C(1,0)、A(-3,0)、B(0,4),设y=a(x+3)(x-1),
将B(0,4)代入,求得a=-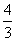 .
.
∴抛物线为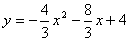
若取C(-1,0)、A(-3,0)、B(0,4),设y=a(x+3)(x+1),将B(0,4)代入,
求得a=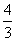
∴抛物线为y=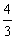 x
x +
+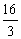 x+4
x+4
⑶如图,过C作CD⊥AB于D,则tan∠ABC=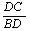
∵ Sin∠BAO=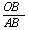 =
=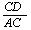 ,cos∠BAO=
,cos∠BAO=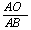 =
=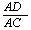
∴ 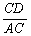 =
= , DC=
, DC=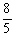 ,
,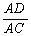 =
=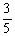 ,AD=
,AD=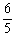 ,…………10分
,…………10分
∴BD=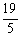
∴tan∠ABC=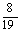


科目:初中数学 来源: 题型:
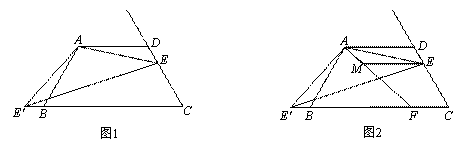
已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'.
(1)如图1,∠AEE'= °;
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
(3)如图3,在(2)的条件下,如果CE=2,AE=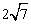 ,求ME的长.
,求ME的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
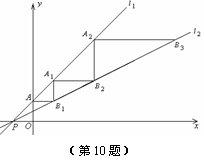
如图,直线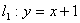 与直线
与直线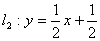 相交于点
相交于点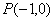 .直线
.直线 与y轴交于点A.一动点
与y轴交于点A.一动点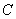 从点A出发,先沿平行于x轴的方向运动,到达直线
从点A出发,先沿平行于x轴的方向运动,到达直线 上的点
上的点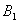 处后,改为垂直于x轴的方向运动,到达直线
处后,改为垂直于x轴的方向运动,到达直线 上的点
上的点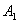 处后,再沿平行于x轴的方向运动,到达直线
处后,再沿平行于x轴的方向运动,到达直线 上的点
上的点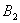 处后,又改为垂直于x轴的方向运动,到达直线
处后,又改为垂直于x轴的方向运动,到达直线 上的点
上的点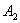 处后,仍沿平行于x轴的方向运动,…… 照此规律运动,动点
处后,仍沿平行于x轴的方向运动,…… 照此规律运动,动点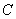 依次经过点
依次经过点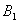 ,
,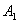 ,
,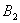 ,
,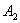 ,
,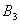 ,
,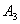 ,…,
,…,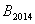 ,
,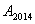 ,…
,…
则当动点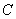 到达
到达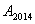 处时,运动的总路径的长为( )(根据2011江干区模拟改编)
处时,运动的总路径的长为( )(根据2011江干区模拟改编)
A.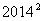 B.
B.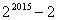 C.
C.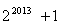 D.
D.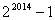
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知△ABC,用直尺和圆规,根据下列要求作图(保留作图痕迹,不写作法)
(1)作∠ABC的平分线BD交AC于点D;
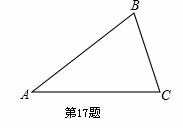 (2)作线段BD的垂直平分线交AB于点E,交BC于点F。由(1)(2)可得,你发现了BEDF是什么四边形?(原创)
(2)作线段BD的垂直平分线交AB于点E,交BC于点F。由(1)(2)可得,你发现了BEDF是什么四边形?(原创)
查看答案和解析>>
科目:初中数学 来源: 题型:
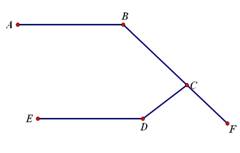
如图,是某交通地图路线,其中AB∥DE,测得∠B=130°,∠DCF=105°,则∠C的度数为( )
A. 155° B. 125°
C.140° D.135°
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
在△ABC中,∠C=90°,AC=12,BC=5,现在AC为轴旋转一周得到一个圆锥。则该圆锥的侧面积为 ( )
(A)130π (B)90π (C)25π (D)65π
查看答案和解析>>
科目:初中数学 来源: 题型:
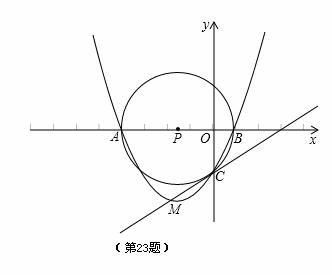
如图,在平面直角坐标系中,坐标原点为O,A点坐标为(-4,0),B点坐标为(1,0),以AB的中点P为圆心,AB为直径作⊙P与y轴的负半轴交于点C.
(1)求经过A、B、C三点的抛物线对应的函数表达式;
(2)设M为(1)中抛物线的顶点,试说明直线MC与⊙P的位置关系,并证明你的结论;
(3)在第二象限中是否存在的一点Q,使得以A,O,Q为顶点的三角形与△OBC相似。若存在,请求出所有满足的Q点坐标;若不存在,请说明理由。(根据2007烟台试卷改编)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com