Question

如图，已知长方形的长为8，宽为4，将长方形沿一条对角线折起压平．则重叠部分（阴影部分）的面积是

1. A.
   10
2. B.
   12
3. C.
   14
4. D.
   16

Answer 1

A
分析：结合图形和题意，可知FB=FC，AF=8-FB（CF），EB=4，根据勾股定理可以推出CF的长度，即可求出阴影部分的面积．
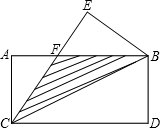
解答：解：∵已知长方形的长为8，宽为4，
∴AF=8-FB，
∵FB=CF，
∴AF=8-CF，
∵AC=4，
∴在Rt△ACF中，
∵CF²=AC²+AF²，即CF²=4²+（8-CF）²，
解得：CF=5，
∴阴影部分的面积=CF×BF÷2=5×4÷2=10．
故选择A．
点评：本题主要考查翻转变换的性质、勾股定理、三角形的面积公式，解题的关键在于求出底边CF和高BE的长度．