【题目】在平面直角坐标系中，点A的坐标为(1，0)，点B的坐标为(m，5﹣m)，当AB的长最小时，m的值为_____
100分闯关期末冲刺系列答案科目：初中数学 来源： 题型：
【题目】某厂改进工艺降低了某种产品的成本，两个月内从每件产品250元，降低到了每件160元，平均每月降低率为（ ）
A.15%
B.20%
C.5%
D.25%
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某地下车库出口处安装了“两段式栏杆”，如图1所示，点A是栏杆转动的支点，点E是栏杆两段的联结点.当车辆经过时，栏杆AEF最多只能升起到如图2所示的位置，其示意图如图3所示（栏杆宽度忽略不计），其中AB⊥BC，EF∥BC，∠AEF=143°，AB=AE=1.2米，那么适合该地下车库的车辆限高标志牌为（ ）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】截止北京时间2020年4月13日，全球新冠肺炎感染者者达1850000人，数据“1850000”用科学记数法表示为（ ）
A.1.85×104B.1.85×105C.1.85×106D.1.85×107
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列性质中，等腰三角形具有而直角三角形不一定具有的是（ ）
A.任意两边之和大于第三边
B.内角和等于180°
C.有两个锐角的和等于90°
D.有一个角的平分线垂直于这个角的对边
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明和几位同学做手的影子游戏时，发现对于同一物体，影子的大小与光源到物体的距离有关.因此，他们认为：可以借助物体的影子长度计算光源到物体的位置.于是，他们做了以下尝试.
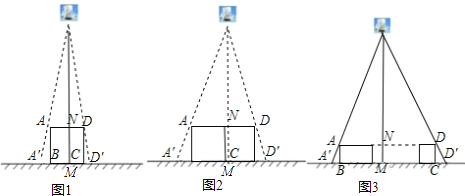
（1）如图1，垂直于地面放置的正方形框架ABCD，边长AB为30cm，在其正上方有一灯泡，在灯泡的照射下，正方形框架的横向影子A′B，D′C的长度和为6cm.那么灯泡离地面的高度为 .
（2）不改变图1中灯泡的高度，将两个边长为30cm的正方形框架按图2摆放，请计算此时横向影子A′B，D′C的长度和为多少？
（3）有n个边长为a的正方形按图3摆放，测得横向影子A′B，D′C的长度和为b，求灯泡离地面的距离.（写出解题过程，结果用含a，b，n的代数式表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列等式 
=1﹣ 
， 
= ﹣ 
， 
= ﹣ 
，把以上三个等式两边分别相加得： + + =1﹣ + ﹣ + ﹣ =1﹣ = 
．
（1）猜想并写出： 
= ．
（2）直接写出下列各式的计算结果：
① + + +…+ 
=；
② + + +…+ = ．
（3）探究并计|算： 
+…+ 
．
查看答案和解析>>
科目：初中数学 来源： 题型：
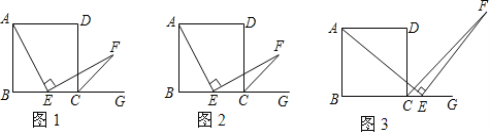
【题目】数学课上,张老师出示了问题：如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°，且EF交正方形外角∠DCG的平分线CF于点F，求证：AE=EF.
经过思考,小明展示了一种正确的解题思路：在AB上截取BM=BE,连接ME，则AM=EC,易证△AME≌△ECF，所以AE=EF.
在此基础上，同学们作了进一步的研究：
(1)小颖提出：如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为小颖的观点正确吗?如果正确，写出证明过程；如果不正确，请说明理由；
(2)小华提出：如图3,点E是BC的延长线上(除C点外)的任意一点，其他条件不变，结论“AE=EF”仍然成立。你认为小华的观点正确吗?如果正确，写出证明过程；如果不正确，请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
