
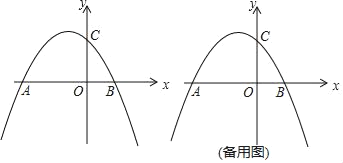
【题目】如图,二次函数y=﹣![]() x2+bx+2的图象与x轴交于点A、B,与y轴交于点C,点A的坐标为(﹣4,0),P是抛物线上一点(点P与点A、B、C不重合).
x2+bx+2的图象与x轴交于点A、B,与y轴交于点C,点A的坐标为(﹣4,0),P是抛物线上一点(点P与点A、B、C不重合).
(1)b= ,点B的坐标是 .
(2)连接AC、BC,判断∠CAB和∠CBA的数量关系,并说明理由.
(3)设点M在二次函数图象上,以M为圆心,半径为![]() 的圆与直线AC相切,求M点的坐标.
的圆与直线AC相切,求M点的坐标.
【答案】(1)﹣![]() ;(
;(![]() ,0);(2)∠CBA=2∠CAB,理由详见解析;(3)点M坐标为(﹣6,﹣5)或(2,﹣1)
,0);(2)∠CBA=2∠CAB,理由详见解析;(3)点M坐标为(﹣6,﹣5)或(2,﹣1)
【解析】
(1)将点![]() 代入函数解析式即可得b的值;令
代入函数解析式即可得b的值;令![]() 解一元二次方程可得出点B坐标;
解一元二次方程可得出点B坐标;
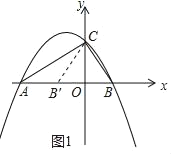
(2)如图1(见解析),作点B关于y轴的对称点![]() ,连接
,连接![]() ,先根据轴对称的性质、等腰三角形的性质可得
,先根据轴对称的性质、等腰三角形的性质可得![]() ,再根据二次函数的解析式求出点C坐标,然后根据点
,再根据二次函数的解析式求出点C坐标,然后根据点![]() 坐标可得
坐标可得![]() ,最后根据等腰三角形的性质、三角形的外角性质即可得出答案;
,最后根据等腰三角形的性质、三角形的外角性质即可得出答案;
(3)先求出点C坐标,从而得出直线AC的解析式,再根据圆的切线的性质得出MD长,从而可得![]() 的面积,然后分两种情况:点M在直线AC上方和点M在直线AC下方,分别根据
的面积,然后分两种情况:点M在直线AC上方和点M在直线AC下方,分别根据![]() 的面积列出等式,求解即可得.
的面积列出等式,求解即可得.
(1)∵二次函数![]() 的图象经过点
的图象经过点![]()
![]()
解得![]()
则二次函数解析式为![]()
令![]() ,解得
,解得![]()
![]()
故答案为:![]() ;
;![]() ;
;
(2)![]() ,理由如下:
,理由如下:
如图1,作点B关于y轴的对称点![]() ,连接
,连接![]() ,则
,则![]()
![]()
![]()
当![]() 时,
时,![]()
![]()
又![]()
![]()
![]()
![]()
![]()
![]() ;
;
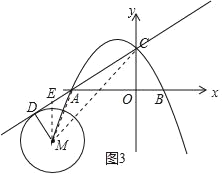
(3)连接![]() ,过点M作
,过点M作![]() 轴,交AC于点E,设圆M与直线AC相切于点D
轴,交AC于点E,设圆M与直线AC相切于点D
![]()
![]()
∴直线AC解析式为![]() ,
,![]()
![]()
设点![]() ,则
,则![]()
①如图2,当点M在直线AC上方时,![]()
![]()
![]()
整理得![]()
此方程的根的判别式![]() ,方程无实数根
,方程无实数根
②如图3和图4,当点M在直线AC下方时,![]() 或
或![]()
![]()
![]()
整理得![]()
解得![]() 或
或![]()
当![]() 时,
时,![]() ,则点M坐标为
,则点M坐标为![]()
当![]() 时,
时,![]() ,则点M坐标为
,则点M坐标为![]()
综上,点M坐标为![]() 或
或![]() .
.




 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数( )
①位似图形都相似:
②两个等边三角形一定是位似图形;
③两个相似多边形的面积比为5:9.则周长的比为5:9;
④两个大小不相等的圆一定是位似图形.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC为等边三角形,点D为BC边上一点,连接AD,并将线段AD绕点A逆时针旋转60°得到AE,连接CE
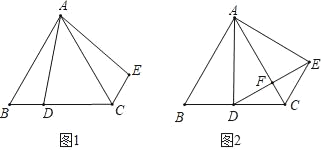
(1)求证:∠ADB=∠AEC;
(2)如图2,当点D为BC中点时,连接DE交AC于点F,直接写出长度等于![]() CF的所有线段.
CF的所有线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每个人都应怀有对水的敬畏之心,从点滴做起,节水、爱水,保护我们生活的美好世界.某地近年来持续干旱,为倡导节约用水,该地采用了“阶梯水价”计费方法,具体方法:每户每月用水量不超过4吨的每吨2元;超过4吨而不超过6吨的,超出4吨的部分每吨4元;超过6吨的,超出6吨的部分每吨6元.该地一家庭记录了去年12个月的月用水量如下表,下列关于用水量的统计量不会发生改变的是( )
用水量x(吨) | 3 | 4 | 5 | 6 | 7 |
频数 | 1 | 2 | 5 | 4﹣x | x |
A. 平均数、中位数 B. 众数、中位数 C. 平均数、方差 D. 众数、方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由![]() 改为
改为![]() ,已知原传送带
,已知原传送带![]() 长为
长为![]() 米.
米.
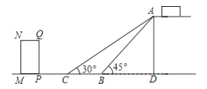
(1)求新传送带![]() 的长度;
的长度;
(2)如果需要在货物着地点![]() 的左侧留出2米的通道,试判断距离
的左侧留出2米的通道,试判断距离![]() 点5米的货物
点5米的货物![]() 是否需要挪走,并说明理由.(参考数据:
是否需要挪走,并说明理由.(参考数据:![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=ax+b与x轴交于点A(4,0),与y轴交于点B(0,﹣2),与反比例函数y=![]() (x>0)的图象交于点C(6,m).
(x>0)的图象交于点C(6,m).
(1)求直线和反比例函数的表达式;
(2)连接OC,在x轴上找一点P,使△OPC是以OC为腰的等腰三角形,请求出点P的坐标;
(3)结合图象,请直接写出不等式![]() ≥ax+b的解集.
≥ax+b的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品现在的售价为每件60元,每星期可卖出300件. 市场调查反映:如调整价格,每降价1元,每星期可多卖出20件. 已知商品的进价为每件40元,如何定价才能使利润最大?这个最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com