
【题目】如图,直线![]() :
:![]() ,点
,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,
为圆心,![]() 长为半径画弧交
长为半径画弧交![]() 轴负半轴于点
轴负半轴于点![]() ;再过点
;再过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,
为圆心,![]() 长为半径画弧交
长为半径画弧交![]() 轴负半轴于点
轴负半轴于点![]() ;…,按此作法进行下去.点
;…,按此作法进行下去.点![]() 的坐标为__________.
的坐标为__________.
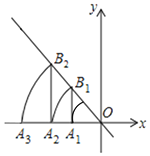
【答案】(-22019,0)
【解析】
先根据一次函数解析式求出B1点的坐标,再根据B1点的坐标求出OA2的长,用同样的方法得出OA3,OA4的长,以此类推,总结规律便可求出点A2020的坐标.
解:∵点A1坐标为(-1,0),
∴OA1=1,
∵在![]() 中,当x=-1时,y=
中,当x=-1时,y=![]() ,即B1点的坐标为(-1,
,即B1点的坐标为(-1,![]() ),
),
∴由勾股定理可得OB1=![]() =2,即OA2=2,
=2,即OA2=2,
即点A2的坐标为(-2,0),即(-21,0),
∴B2的坐标为(-2,![]() ),
),
同理,点A3的坐标为(-4,0),即(-22,0),
点B3的坐标为(-4,![]() ),
),
以此类推便可得出:点A2020的坐标为(-22019,0).
故答案为:(-22019,0).


科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
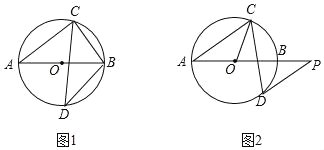
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BAC=40°.
(1)如图1,若D为弧AB的中点,求∠ABC和∠ABD的度数;
(2)如图2,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过![]() km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方
km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方![]() m处,过了2s后,测得小汽车与车速检测仪间距离为
m处,过了2s后,测得小汽车与车速检测仪间距离为![]() m,这辆小汽车超速了吗?
m,这辆小汽车超速了吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
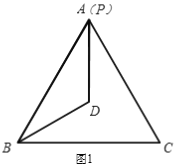
【题目】已知△ABC是等边三角形,P为△ABC所在平面内一个动点,BP=BA,若0°﹤∠PBC﹤ 180°,且∠PBC的平分线上一点D满足DB=DA.
(1)当BP和BA重合时(如图1),则∠BPD=______°.
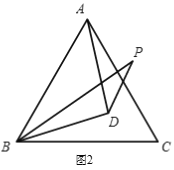
(2)当BP在∠ABC内部时(如图2),求∠BPD的度数
(3)当BP在∠ABC外部时,请直接写出∠BPD的度数,并画出相应的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
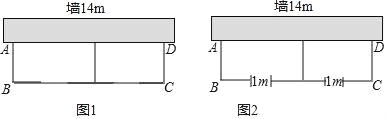
【题目】如图,有长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,有以下两种围法.
(1)如图1,设花圃的宽AB为x米,面积为y米2,求y与x之间的含函数表达式,并确定x的取值范围;
(2)如图2,为了方便出入,在建造篱笆花圃时,在BC上用其他材料造了宽为1米的两个小门,设花圃的宽AB为a米,面积为S米2,求S与a之间的函数表达式及S的最大值?
查看答案和解析>>
科目:初中数学 来源: 题型:
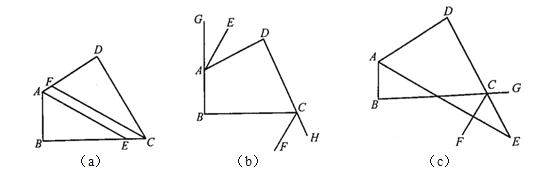
【题目】在四边形![]() 中,
中,![]() ,
,
(1)如图(a)所示,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的角平分线,判断
的角平分线,判断![]() 与
与![]() 的位置关系,并证明.
的位置关系,并证明.
(2)如图(b)所示,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的角平分线,直接写出
的角平分线,直接写出![]() 与
与![]() 的位置关系.
的位置关系.
(3)如图(c)所示,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的角平分线,判断
的角平分线,判断![]() 与
与![]() 的位置关系,并证明.
的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两张完全相同的矩形纸片![]() 、
、![]() 按如图方式放置,
按如图方式放置,![]() 为重合的对角线.重叠部分为四边形
为重合的对角线.重叠部分为四边形![]() ,
,

![]() 试判断四边形
试判断四边形![]() 为何种特殊的四边形,并说明理由;
为何种特殊的四边形,并说明理由;
![]() 若
若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队承包一项工程,如果甲工程队单独施工,恰好如期完成;如果乙工程队单独施工就要超过6个月才能完成,现在甲、乙两队先共同施工4个月,剩下的由乙队单独施工,则恰好如期完成.
(1)问原来规定修好这条公路需多少长时间?
(2)现要求甲、乙两个工程队都参加这项工程,但由于受到施工场地条件限制,甲、乙两工程队不能同时施工.已知甲工程队每月的施工费用为4万元,乙工程队每月的施工费用为2万元.为了结算方便,要求:甲、乙的施工时间为整数个月,不超过15个月完成.当施工费用最低时,甲、乙各施工了多少个月?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com