
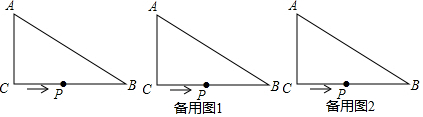
分析 (1)当t=1s时,△ACP是直角三角形,根据公式求△ACP的面积;
(2)如图3,过P作PH⊥AB于H,Rt△PHB中,PB=8-2t,根据勾股定理列方程可求解;
(3)分四种情况进行讨论:
①如图4,根据AC=CP列式求解;
②如图5,根据AC=AP列式求解;
③如图6,AP=PC,根据AP=PB列式求解;
④如图7,AC=CP,根据AP的值列式求解.
解答 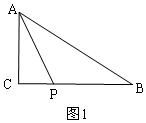 解:(1)如图1,点P在BC上,
解:(1)如图1,点P在BC上,
由题意得:CP=2t,
当t=1时,PC=2,
∴S△ACP=$\frac{1}{2}$AC•PC=$\frac{1}{2}$×6×2=6;
如图2,Rt△ACB中,由勾股定理得:AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
(2)如图3,AP平分∠CAB,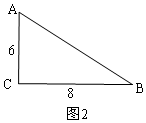
过P作PH⊥AB于H,
∵∠C=90°,
∴PC=PH=2t,
∵∠C=∠AHP=90°,AP=AP,
∴△ACP≌△AHP,
∴AH=AC=6,
∴BH=4,
在Rt△PHB中,PB=8-2t,
∴(2t)2+42=(8-2t)2,
t=$\frac{3}{2}$;
则当t=$\frac{3}{2}$时,线段AP是∠CAB的平分线;
(3)当△ACP是等腰三角形时,有四种情况:
①如图4,AC=CP,2t=6,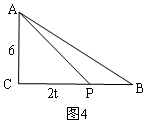
t=3,
②如图5,AC=AP,18-2t=6,
t=6,
③如图6,AP=PC,
过P作PG⊥AC于G,
∵∠C=90°,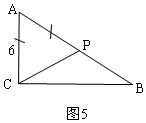
∴PG∥BC,
∴AP=PB,
即18-2t=2t-8,
t=$\frac{13}{2}$,
④如图7,AC=CP,
过C作CM⊥AB于M,
∴AM=PM,
tan∠CAB=$\frac{CM}{AM}=\frac{BC}{AC}=\frac{8}{6}$=$\frac{4}{3}$,
设CM=4x,AM=3x,则AC=5x,
5x=6,
x=$\frac{6}{5}$,
∴AP=6x=6×$\frac{6}{5}$=$\frac{36}{5}$,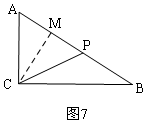
18-2t=$\frac{36}{5}$,
t=5.4,
综上所述,当△ACP是等腰三角形时,t的值是3s或6s或$\frac{13}{2}$s或5.4s.
点评 本题是三角形的综合题,难度适中,考查了动点运动问题、等腰三角形的性质和判定、勾股定理、三角函数、角平分线的性质等知识,首先要确定动点P的运用路程=时间t×速度2,本题在第3问的等腰三角形中采用了分类讨论的思想,注意不要丢解,并利用数形结合的思想解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 2x=196+4(70-x) | B. | 4x+2(70-x)=196 | C. | 2x+4(70-x)=196 | D. | 2x+196=4(70-x) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
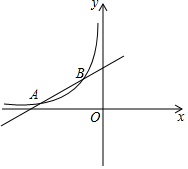 如图,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,求反比例函数的解析式,并根据图象直接回答:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?
如图,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,求反比例函数的解析式,并根据图象直接回答:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
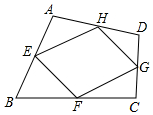 如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )
如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD边的中点,AC=6,BD=8,那么四边形EFGH的周长是( )| A. | 20 | B. | 28 | ||
| C. | 14 | D. | 以上答案均有可能 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com