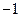已知二次函数中.函数与自变量的部分对应值如下表:----(1)求该二次函数的关系式,(2)当为何值时.有最小值.最小值是多少?(3)若.两点都在该函数的图象上.试比较与的大小．题目和参考答案——青夏教育精英家教网—

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

科目：初中数学 来源： 题型：

在平面直角坐标系xOy中，已知二次函数y=ax²+bx+c（a≠0）的图象与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，其顶点的横坐标为1，且过点（2，3）和（-3，-12）．
（1）求此二次函数的表达式；
（2）若直线l：y=kx（k≠0）与线段BC交于点D（不与点B，C重合），则是否存在这样的直线l，使得以B，O，D为顶点的三角形与△BAC相似？若存在，求出该直线的函数表达式及点D的坐标；若不存在，请说明理由；
（3）若点P是位于该二次函数对称轴右边图象上不与顶点重合的任意一点，试比较

锐角∠PCO与∠ACO的大小（不必证明），并写出此时点P的横坐标x_p的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：

问题（一）：观察函数y=

1

2

x2-x-4的图象，填空：当函数值y＞0时，x的取值范围是

；当函数值y＜0时，x的取值范围是

．
问题（二）：已知二次函数y=（p-3）x²+（10-p²）x+q，当1＜x＜5时，函数值y为正，当x＜1或x＞5时，函数值y为负．
（Ⅰ）求二次函数的解析式；
（Ⅱ）设直线y=

1

2

x+1与二次函数的图象交于点A、B．
（1）求点A、B的坐标，并在给定的直角坐标系中画出直线及二次函数的图象；
（2）设平行于y轴的直线x=t、x=t+2分别交线段AB于点E、F，交二次函数的图象于点H、G（H、G不与A、B重合）．
①求t的取值范围；
②是否能适当选择点E的位置，使四边形EFGH是平行四边形？如果能，求出此时点E的坐标；如果不能，请说明理由．

查看答案和解析>>

科目：初中数学 来源：第6章《二次函数》中考题集（43）：6.4 二次函数的应用（解析版） 题型：解答题

在平面直角坐标系xOy中，已知二次函数y=ax²+bx+c（a≠0）的图象与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，其顶点的横坐标为1，且过点（2，3）和（-3，-12）．
（1）求此二次函数的表达式；
（2）若直线l：y=kx（k≠0）与线段BC交于点D（不与点B，C重合），则是否存在这样的直线l，使得以B，O，D为顶点的三角形与△BAC相似？若存在，求出该直线的函数表达式及点D的坐标；若不存在，请说明理由；
（3）若点P是位于该二次函数对称轴右边图象上不与顶点重合的任意一点，试比较锐角∠PCO与∠ACO的大小（不必证明），并写出此时点P的横坐标x_p的取值范围．

查看答案和解析>>

科目：初中数学 来源：2011年浙江省绍兴市中考数学模拟试卷（解析版） 题型：解答题

在平面直角坐标系xOy中，已知二次函数y=ax²+bx+c（a≠0）的图象与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，其顶点的横坐标为1，且过点（2，3）和（-3，-12）．
（1）求此二次函数的表达式；
（2）若直线l：y=kx（k≠0）与线段BC交于点D（不与点B，C重合），则是否存在这样的直线l，使得以B，O，D为顶点的三角形与△BAC相似？若存在，求出该直线的函数表达式及点D的坐标；若不存在，请说明理由；
（3）若点P是位于该二次函数对称轴右边图象上不与顶点重合的任意一点，试比较锐角∠PCO与∠ACO的大小（不必证明），并写出此时点P的横坐标x_p的取值范围．