
����Ŀ�����˻������ҹ���չѸ�٣�ȫ�����λ���������˻�����Ƶ���װ���Ĵ��ɶ�˫������ɣ��������ܺ������˻���1�����˻��Ӻ���5�״���������1��/����ٶ����������ͬʱ��2�����˻��Ӻ���15�״���������0.5��/����ٶ������������˻�����ʱ��Ϊ![]() �룩��
�룩��
��1�����1�����˻�����λ�õĺ���![]() ���ף���
���ף���![]() ֮��Ĺ�ϵʽ��2�����˻�����λ�õĺ���
֮��Ĺ�ϵʽ��2�����˻�����λ�õĺ���![]() ���ף���
���ף���![]() ֮��Ĺ�ϵʽ��
֮��Ĺ�ϵʽ��
��2����ijһʱ���������˻��ܷ�λ��ͬһ�߶ȣ�����ܣ���������˻�������ʱ����߶ȣ�������ܣ���˵������.
��3����������ʱ�䣬�������˻�����λ�õĺ������5��.
���𰸡�(1) y1=x+5��y2=![]() x+15��(2)20,���ɼ�������(3) 10���30��,���ɼ�����
x+15��(2)20,���ɼ�������(3) 10���30��,���ɼ�����
��������
��1���������⼴�ɵó���Ӧ��ϵʽ��
��2�����ݣ�1���Ľ����з��̽�ɣ�
��3�����ݣ�1���Ľ����з��̽�ɣ�
��1��1�����˻��ĺ���y1���ף���x֮��Ĺ�ϵʽΪy1=x+5��2�����˻��ĺ���y2���ף���x֮��Ĺ�ϵʽΪ��y2=![]() x+15��
x+15��
��2����������ã�x+5=![]() x+15�����x=20��
x+15�����x=20��
���������˻�λ��ͬһ�߶ȣ���˸߶�Ϊ����20�ף�
��3����������ã�x+5-��![]() x+15��=5��
x+15��=5��![]() x+15-��x+5��=5��
x+15-��x+5��=5��
���x=10��x=30��
�ʵ��������˻�����λ�õĺ������5��ʱ������ʱ��Ϊ10���30�룮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ���������ݣ��ٽ�����⣺
���⣺��![]() +
+![]() +
+![]() -
-![]() +
+![]() =
=![]() ����
����![]() ��
��![]() ��ֵ��
��ֵ��
�⣺![]() +
+![]() +
+![]() -
-![]() +
+![]() =
=![]()
![]() +
+![]() +
+![]() +
+![]() -
-![]() +
+![]() =
=![]()
![]() ��
��![]() ��
��![]() +��
+��![]() -
-![]() ��
��![]() =
=![]()
![]() -
-![]() =
=![]()
![]() -
-![]() ��
��![]()
���⣺��1����![]() -
-![]() -
-![]() =
=![]() �� ��
�� ��![]() ��ֵ��
��ֵ��
��2����֪![]() �����߳�
�����߳�![]() ������������������
������������������![]() -
-![]() -
-![]() +
+![]() ��3-
��3-![]() ��=
��=![]() ������
������![]() ��������״�������Σ�
��������״�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬CD��AB�ڵ�D����ACD=3��BCD��E��б��AB���е�,���ECD�Ķ���Ϊ__________��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BD�DZ߳�Ϊ1��������ABCD�ĶԽ��ߣ�BEƽ�֡�DBC��DC�ڵ�E���ӳ�BC����F��ʹCF=CE������DF����BE���ӳ����ڵ�G.
��1����֤����BCE�ա�DCF��
��2����CF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
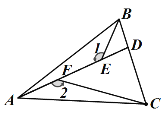
����Ŀ����ͼ����ABCΪ���������Σ�AB��AC��AB��BC����1����2��90�㣬��1����BAC��180�㣬��A��F��E��D��һ��ֱ���ϣ���D��BC���ϣ�CD��2BD.����ABC�����Ϊ40�����ABE���CDF�����֮��________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0���IJ���ͼ����ͼ��ʾ��ͼ����㣨��1��0�����Գ���Ϊֱ��x=2�����н��ۣ���1��4a+b=0����2��9a+c��3b����3��8a+7b+2c��0����4������A����3��y1������B����![]() ��y2������C��
��y2������C��![]() ��y3���ڸú���ͼ���ϣ���y1��y3��y2����5��������a��x+1����x��5��=��3������Ϊx1��x2����x1��x2����x1����1��5��x2��
��y3���ڸú���ͼ���ϣ���y1��y3��y2����5��������a��x+1����x��5��=��3������Ϊx1��x2����x1��x2����x1����1��5��x2��
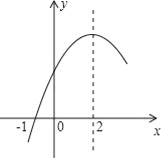
������ȷ���۵������_______________�����ں�������������Ϊ������ȷ���۵���ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��רҵ���ƻ�Ͷ����ֲ���ܼ���ľ�������г�������Ԥ�⣬��ֲ��ľ������y1��Ͷ����x����������ϵ����ֲ���ܵ�����y2��Ͷ����x��ƽ������������ϵ�����õ��˱����е����ݣ�
Ͷ����x����Ԫ�� | 2 |
��ֲ��ľ����y1����Ԫ�� | 4 |
��ֲ��������y2����Ԫ�� | 2 |
��1���ֱ��������y1��y2����Ͷ����x�ĺ�����ϵʽ��
��2�������λרҵ����8��Ԫ�ʽ�Ͷ����ֲ���ܺ���ľ������Ͷ����ֲ���ܽ��m��Ԫ����ֲ���ܺ���ľ����������W��Ԫ��ֱ��д��W����m�ĺ�����ϵʽ�����������ٻ�ö����������ܻ�ȡ����������Ƕ��٣�
��3������רҵ�������������22���ڣ�2���������£�ֱ��д��Ͷ����ֲ���ܵĽ��m�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳���2����DAC��ƽ���߽�DC�ڵ�E������P��Q�ֱ���AD��AE�ϵĶ��㣬��DQ+PQ����СֵΪ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC������A![]() 90����AB
90����AB![]() AC��
AC��
��1����ͼ1����ABC�Ľ�ƽ����BD��CE���ڵ�Q�����жϡ�![]() ���Ƿ���ȷ��________����ǡ�����
���Ƿ���ȷ��________����ǡ�����
��2����P����ABC����ƽ���ڵ�һ��������PA��PB����PB![]()
![]() PA��
PA��
����ͼ2����P�ڡ�ABC������ABP![]() 30��������PAB�Ĵ�С��
30��������PAB�Ĵ�С��
����ͼ3����P�ڡ�ABC��������PC������APC![]() ������BPC
������BPC![]() �����õ�ʽ��ʾ������֮���������ϵ����֤����Ľ�����
�����õ�ʽ��ʾ������֮���������ϵ����֤����Ľ�����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com