
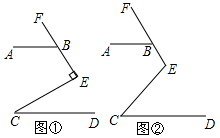
分析 (1)过E作EK∥AB,则∠ABE+∠1=180°,根据AB∥CD,EK∥AB,即可得到EK∥CD,再根据平行线的性质,即可得到∠C的度数;
(2)过E作EK∥AB,则∠ABE+∠1=180°,根据AB∥CD,EK∥AB,即可得到EK∥CD,再根据平行线的性质,即可得到180°-∠ABE+∠C=120°,据此可得∠ABE与∠C的数量关系.
解答 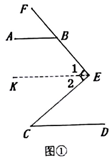 解:(1)如图①,过E作EK∥AB,则∠ABE+∠1=180°,
解:(1)如图①,过E作EK∥AB,则∠ABE+∠1=180°,
∴∠1=180°-∠ABE=50°,
∵∠CEF=90°,
∴∠2=90°-∠1=40°,
∵AB∥CD,EK∥AB,
∴EK∥CD,
∴∠C=∠2=40°;
(2)∠ABE-∠C=60°,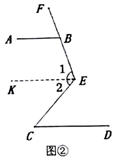
理由:如图②,过E作EK∥AB,则∠ABE+∠1=180°,
∴∠1=180°-∠ABE,
∵AB∥CD,EK∥AB,
∴EK∥CD,
∴∠C=∠2,
∵∠CEF=∠1+∠2=120°,即180°-∠ABE+∠C=120°,
∴∠ABE-∠C=180°-120°=60°.
点评 本题主要考查了平行线的性质,解题时注意:两直线平行,同旁内角互补;两直线平行,内错角相等.解决问题的关键是作辅助线构造同旁内角以及内错角.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
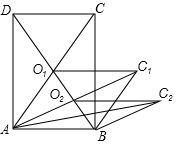 如图所示,矩形ABCD的面积为12cm2,它的两条对角线交于点O1,以AB、AO1邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2;同样以AB、AO2为邻边作平行四边形ABC2O2…;依此类推,则平行四边形ABC6O6的面积为$\frac{3}{16}$cm2.
如图所示,矩形ABCD的面积为12cm2,它的两条对角线交于点O1,以AB、AO1邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2;同样以AB、AO2为邻边作平行四边形ABC2O2…;依此类推,则平行四边形ABC6O6的面积为$\frac{3}{16}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
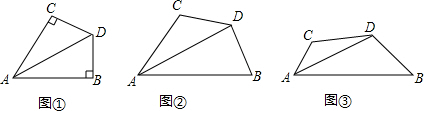
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
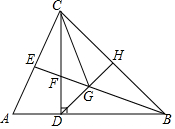 如图,在△ABC中,AB=BC,BE平分∠ABC,CD⊥AB于点D,CD=BD,点H是BC边的中点,连接DH,交BE于点G,连接CG.
如图,在△ABC中,AB=BC,BE平分∠ABC,CD⊥AB于点D,CD=BD,点H是BC边的中点,连接DH,交BE于点G,连接CG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
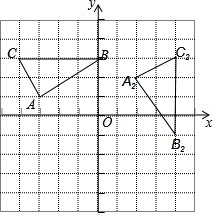 如图,平面直角坐标系中,已知A(-3,1)、B(0,3)、C(-4,3).
如图,平面直角坐标系中,已知A(-3,1)、B(0,3)、C(-4,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
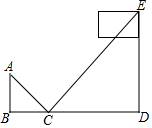 处看到旗杆顶部E,此时小军的站立点B与点C的水平距离为2m,旗杆底部D与点C的水平距离为12m.若小军的眼睛距离地面的高度为1.5m(即AB=1.5m),则旗杆的高度为9m.
处看到旗杆顶部E,此时小军的站立点B与点C的水平距离为2m,旗杆底部D与点C的水平距离为12m.若小军的眼睛距离地面的高度为1.5m(即AB=1.5m),则旗杆的高度为9m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com