【题目】已知
、
，添加下列条件后，不能判断四边形
为菱形的是（ ）
A. 
平分
B. 
且
C. 为中线
D. 
【答案】C
【解析】
首先根据题意画出图形，然后由DE∥AC、DF∥AB，判定四边形DEAF为平行四边形，再由菱形的判定定理求解即可求得答案；注意掌握排除法在选择题中的应用．
如图所示：
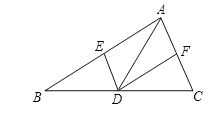
∵DE∥AC、DF∥AB，
∴四边形DEAF为平行四边形，
A选项：∵AD平分∠BAC，DF∥AB，
∴∠BAD=∠CAD，∠BAD=∠ADF，
∴∠CAD=∠ADF，
∴AF=DF，
∴四边形DEAF为菱形；
B选项：∵AB=AC且BD=CD，
∴AD平分∠BAC，
同理可得：四边形DEAF为菱形；
C选项：∵由AD为中线，得不到AD平分∠BAC，证不出四边形DEAF的邻边相等，
∴不能判断四边形DEAF为菱形；
D选项：∵AD⊥EF，
∴平行四边形DEAF是菱形．
故选：C．
一线名师权威作业本系列答案科目：初中数学 来源： 题型：
【题目】如图，正方形
中，点
是
上任意一点，以
为边作正方形
．
①连接
，求证：
；
②连接
，猜想
的度数，并证明你的结论；
③设点在线段上运动，
，正方形的面积为
，正方形的面积为
，试求与
的函数关系式，并写出的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，点
是
边上（端点除外）的一个动点，过点作直线
．设
交
的平分线于点
，交的外角平分线于点
，连接
、
．
那么当点运动到何处时，四边形
是矩形？并说明理由．
在的前提下满足什么条件，四边形是正方形？（直接写出答案，无需证明）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是某同学对多项式（x2－4x+2）（x2－4x+6）+4进行因式分解的过程．
解：设x2－4x=y
原式=（y+2）（y+6）+4 （第一步）
= y2+8y+16 （第二步）
=（y+4）2 （第三步）
=（x2－4x+4）2 （第四步）
回答下列问题：
（1）该同学第二步到第三步运用了因式分解的_______．
A．提取公因式 B．平方差公式 C．两数和的完全平方公式 D．两数差的完全平方公式
（2）该同学因式分解的结果是否彻底？________．（填“彻底”或“不彻底”）
若不彻底，请直接写出因式分解的最后结果_________．
（3）请你模仿以上方法尝试对多项式（x2－2x）（x2－2x+2）+1进行因式分解．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在四边形
中，点
、
是对角线
上的两点，且
．则下列结论中，错误的是（ ）
A. 若四边形
是平行四边形，则也是平行四边形
B. 若四边形是菱形，则四边形也是菱形
C. 若四边形是矩形，则四边形也是矩形
D. 若四边形是正方形，则四边形一定是菱形
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，AB∥CD，∠1=∠2，DB=DC．
（1）求证：△ABD≌△EDC；
（2）若∠A=135°，∠BDC=30°，求∠BCE的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
