
 如图,四边形ABCD中,AC、BD交于O点且AC⊥BD,AB、CD所在的直线为l1、l2,l1∥l2.若AC=8,BD=6,固定线段AC不动,线段BD在l1、l2之间平移.
如图,四边形ABCD中,AC、BD交于O点且AC⊥BD,AB、CD所在的直线为l1、l2,l1∥l2.若AC=8,BD=6,固定线段AC不动,线段BD在l1、l2之间平移.分析 (1)可用排除法;
(2)由于梯形的两底是关于x的一元二次方程的两个根,所以△>0,可考虑根与系数的关系.过点A作AE∥BD,交CD的延长线于点E,则四边形ABDE是平行四边形,△ACE是直角三角形,其斜边恰好是上下底的和,两条直角边是梯形的两条对角线,先求出m的值,再确定n的取值范围.
(3)由(2)知,梯形上下底的和为m,若要证明梯形两个腰的和大于两个底的和,由于本题梯形的对角线互相垂直,可考虑利用直角三角形斜边上的中线与斜边的关系以及梯形的中位线定理.故作梯形的中位线,并连接各中点和O构造三角形,利用三边关系求解.
解答 解:(1)∵四边形ABCD的一组对边平行,一组对边相等,
∴该四边形是平行四边形或者是等腰梯形.
∵等腰梯形的对角线相等,所以四边形ABCD是平行四边形.
因为?ABCD的两条对角线互相垂直且不相等,
∴该四边形是菱形.
故答案为:菱形.
(2)如图.过点A作AE∥BD,交CD的延长线于点E.
∵AB∥CD,AE∥BD,
∴四边形ABDE是平行四边形.
∴AB=DE,BD=AE=6,∠CAE=∠COD=90°.
在RT△ACE中,由于AC=8,AE=6,
∴CE=10,即AB+CD=10.
∵AB、CD长为关于x方程x2-mx+2n-3=0两根,
∴△=m2 -4(n-3)>0,AB+CD=m=10,
即102-4n+12>0,所以n<28.
∵AB×CD=2n-3>0,
∴n>1.5.
∴1.5<n<28.
(3)若BC、AD的中点分别为M、N,连接0M、0N、MN.
在RT△BOC、RT△AOD中,2OM=BC,2ON=AD.
在△OMN中,OM+0N>MN,
∴BC+AD>2MN.
∵MN是梯形ABCD的中位线,
所以2MN=AB+CD,
由(2)知AB+CD=m,
∴2MN=m.
∴BC+AD>m.
点评 点评:本题是梯形、平行四边形相关知识与一元二次方程相结合的综合性题目.考察了梯形的中位线定理、直角三角形斜边的中线、四边形的判定、勾股定理、平行四边形的判定和性质以及一元二次方程的根的判别式和根与系数的关系.解决本题目的关键是通过作辅助线,把分散的条件集中起来综合考虑.


科目:初中数学 来源: 题型:选择题
| A. | 每天比原计划多铺设10米,结果延期15天才完成 | |
| B. | 每天比原计划少铺设10米,结果延期15天才完成 | |
| C. | 每天比原计划多铺设10米,结果提前15天才完成 | |
| D. | 每天比原计划少铺设10米,结果提前15天才完成 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
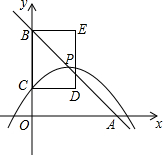 如图,在平面直角坐标系中,直线y=-x+4与x轴、y轴分别交于点A、B.抛物线y=-$\frac{1}{3}{(x-m)^2}$+n的顶点P在直线y=-x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.
如图,在平面直角坐标系中,直线y=-x+4与x轴、y轴分别交于点A、B.抛物线y=-$\frac{1}{3}{(x-m)^2}$+n的顶点P在直线y=-x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com