
【题目】(2014浙江金华)如图,矩形ABOD的两边OB,OD都在坐标轴的正半轴上,OD=3,另两边与反比例函数![]() (k≠0)的图象分别相交于点E、F,且DE=2.过点E作EH⊥x轴于点H,过点F作FG⊥EH于点G.回答下面的问题:
(k≠0)的图象分别相交于点E、F,且DE=2.过点E作EH⊥x轴于点H,过点F作FG⊥EH于点G.回答下面的问题:
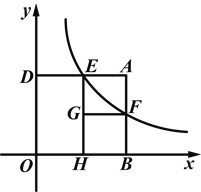
(1)①求反比例函数的解析式.
②当四边形AEGF为正方形时,求点F的坐标.
(2)小亮进一步研究四边形AEGF的特征后提出问题:“当AE>EG时,矩形AEGF与矩形DOHE能否全等?能否相似?”
针对小亮提出的问题,请你判断这两个矩形能否全等(直接写出结论即可).这两个矩形能否相似?若能相似,求出相似比;若不能相似,试说明理由.
【答案】(1)①![]() ②F(3,2) (2)不能全等
②F(3,2) (2)不能全等
【解析】(1)①∵四边形ABOD为矩形,EH⊥x轴,OD=3,DE=2,
∴E点坐标为(2,3).
∴k=2×3=6.
∴反比例函数解析式为![]() .
.
②设正方形AEGF的边长为a,则AE=AF=a,
∴A点坐标为(2+a,3),F点坐标为(2+a,3-a).
把点F的坐标代入![]() ,得(2+a)(3-a)=6,
,得(2+a)(3-a)=6,
解得a1=1,a2=0(舍去),
∴F点的坐标为(3,2).
(2)当AE>EG时,矩形AEGF与矩形DOHE不能全等.
理由如下:
假设矩形AEGF与矩形DOHE全等,则AE=OD=3,AF=DE=2,
∴A点坐标为(5,3),
∴F点坐标为(5,1),而5×1=5≠6,
∴F点不在反比例函数![]() 的图象上,
的图象上,
∴矩形AEGF与矩形DOHE不能全等.
当AE>EG时,矩形AEGF与矩形DOHE能相似.
由矩形AEGF与矩形DOHE相似,
得AE︰OD=AF︰DE,
∴![]() ,
,
设AE=3t,则AF=2t,
∴A点坐标为(2+3t,3),
∴F点坐标为(2+3t,3-2t),
把点F的坐标代入![]() ,得(2+3t)(3-2t)=6,
,得(2+3t)(3-2t)=6,
解得t1=0(舍去), ![]() ,
,
∴![]() ,
,
∴矩形AEGF与矩形DOHE的相似比为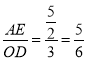 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知经过原点的抛物线![]() 与
与![]() 轴的另一个交点为
轴的另一个交点为![]() ,现将抛物线向右平移
,现将抛物线向右平移![]() 个单位长度,所得抛物线与
个单位长度,所得抛物线与![]() 轴交于
轴交于![]() ,与原抛物线交于点
,与原抛物线交于点![]() ,设
,设![]() 的面积为
的面积为![]() ,则用
,则用![]() 表示
表示![]() =__________
=__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小晗家客厅装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小晗按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.
(1)若小晗任意按下一个开关,正好楼梯灯亮的概率是多少?
(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图或列表法加以说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
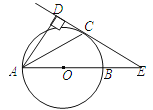
【题目】如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
(1)求证:直线CD为⊙O的切线;
(2)当AB=2BE,且CE=时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=﹣x2+4x﹣3,把抛物线C1先向右平移3个单位长度,再向上平移3个单位长度,得到抛物线C2, 将抛物线C1和抛物线C2这两个图象在x轴及其上方的部分记作图象M.若直线y=kx+ ![]() (k≥0)与图象M至少有2个不同的交点,则k的取值范围是________.
(k≥0)与图象M至少有2个不同的交点,则k的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点的坐标为(![]() ,1),下列结论:①c>0;②b2﹣4ac>0;③a+b=0;④4ac﹣b2>4a,其中错误的是( )
,1),下列结论:①c>0;②b2﹣4ac>0;③a+b=0;④4ac﹣b2>4a,其中错误的是( )
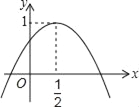
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A,B,与
与x轴交于点A,B,与![]() 轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。
轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。

(1)求该抛物线的解析式;
(2)求梯形COBD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
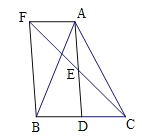
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:△AEF≌△DEC;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com