
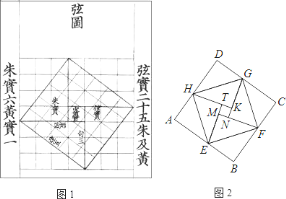
【题目】汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图![]() ).图
).图![]() 是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形
是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形![]() 、正方形
、正方形![]() 、正方形
、正方形![]() 的面积分别为
的面积分别为![]() 、
、![]() 、
、![]() .若
.若![]() ,则
,则![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】我校初三学子在不久前结束的体育中考中取得满意成绩,赢得2016年中考开门红.现随机抽取了部分学生的成绩作为一个样本,按A(满分)、B(优秀)、C(良好)、D(及格)四个等级进行统计,并将统计结果制成如下2幅不完整的统计图,如图,请你结合图表所给信息解答下列问题: 
(1)将折线统计图在图中补充完整;此次调查共随机抽取了名学生,其中学生成绩的中位数落在等级;
(2)为了今后中考体育取得更好的成绩,学校决定分别从成绩为满分的男生和女生中各选一名参加“经验座谈会”,若成绩为满分的学生中有4名女生,且满分的男、女生中各有2名体育特长生,请用列表或画树状图的方法求出所选的两名学生刚好都不是体育特长生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
(1)如图1,当E是线段AC的中点,且AB=2时,求△ABC的面积;
(2)如图2,当点E不是线段AC的中点时,求证:BE=EF;
(3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解2014年某地区10万名大、中、小学生50米跑成绩情况,教育部门从这三类学生群体中各抽取了10%的学生进行检测,整理样本数据,并结合2010年抽样结果,得到下列统计图: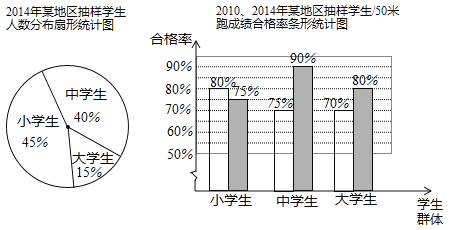
(1)本次检测抽取了大、中、小学生共 名,其中小学生 名;
(2)根据抽样的结果,估计2014年该地区10万名大、中、小学生中,50米跑成绩合格的中学生人数为 名;
(3)比较2010年与2014年抽样学生50米跑成绩合格率情况,写出一条正确的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),![]() ,
,![]() ,从三角板的刻度可知
,从三角板的刻度可知![]() ,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为________
,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为________![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为________________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点A(﹣2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α. 
(1)如图①,当α=90°时,求AE′,BF′的长;
(2)如图②,当α=135°时,求证AE′=BF′,且AE′⊥BF′;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0),B(4,0),C(0,2)三点. 
(1)求这条抛物线的解析式;
(2)E为抛物线上一动点,是否存在点E,使以A、B、E为顶点的三角形与△COB相似?若存在,试求出点E的坐标;若不存在,请说明理由;
(3)若将直线BC平移,使其经过点A,且与抛物线相交于点D,连接BD,试求出∠BDA的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com