
分析 根据已知条件得到△ADE∽△ABC,由相似三角形的性质得到$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AD}{AB}$)2=$\frac{1}{8}$,求得AB:AD=2$\sqrt{2}$:1;于是得到$\frac{BD}{AD}$=$\frac{2\sqrt{2}-1}{1}$,求得$\frac{{S}_{△BDE}}{{S}_{△ADE}}$=$\frac{2\sqrt{2}-1}{1}$,于是得到结论.
解答 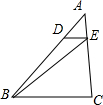 解:如图,∵DE∥BC,
解:如图,∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AD}{AB}$)2=$\frac{1}{8}$,
∴AB:AD=2$\sqrt{2}$:1;
∴$\frac{BD}{AD}$=$\frac{2\sqrt{2}-1}{1}$,
∴$\frac{{S}_{△BDE}}{{S}_{△ADE}}$=$\frac{2\sqrt{2}-1}{1}$,
∴$\frac{{S}_{△ABC}}{{S}_{△BDE}}$=$\frac{8}{2\sqrt{2}-1}$=$\frac{16\sqrt{2}-8}{7}$.
故答案为:2$\sqrt{2}$:1,$\frac{16\sqrt{2}-8}{7}$.
点评 本题考查了相似三角形的判定和性质,知道不等底同高的三角形的面积比等于底的比是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,网格中每个小正方形的边长均为1,线段AB的顶点在校正方形的顶点上,按要求画出图形.
如图,网格中每个小正方形的边长均为1,线段AB的顶点在校正方形的顶点上,按要求画出图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 圆柱的高为16cm,底面半径为2cm,点B离地面8cm,一只蜘蛛以5cm/s的速度从底面上的点A处绕曲面到达点B捕食被网到的昆虫,蜘蛛到昆虫所在点B所用最短时间是多少?(π取3)
圆柱的高为16cm,底面半径为2cm,点B离地面8cm,一只蜘蛛以5cm/s的速度从底面上的点A处绕曲面到达点B捕食被网到的昆虫,蜘蛛到昆虫所在点B所用最短时间是多少?(π取3)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC内接于⊙O,弦AB的垂直平分线OD与AB、BC分别相交于点M、N,与AC的延长线相交于点P,与⊙O相交于点D,求证:(1)ON•PN=NB•CN(2)OB2=ON•OP.
如图,△ABC内接于⊙O,弦AB的垂直平分线OD与AB、BC分别相交于点M、N,与AC的延长线相交于点P,与⊙O相交于点D,求证:(1)ON•PN=NB•CN(2)OB2=ON•OP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com