
 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动.设△PQD的面积为S,点移动的时间为x(x>0)
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动.设△PQD的面积为S,点移动的时间为x(x>0)分析 (1)用矩形的面积减去三个直角三角形的面积即可得出结果;
(2)S是x的二次函数,配方后即可得出结论.
解答 解:(1)根据题意得:AP=x,BQ=2x,
则BP=6-x,CQ=12-2x,
∴△PQD的面积S=矩形ABCD的面积-△APD的面积-△PBQ的面积-△CDQ的面积
=12×6-$\frac{1}{2}$×12x-$\frac{1}{2}$•2x(6-x)-$\frac{1}{2}$×6(12-2x)
=x2-6x+36,
∴S=x2-6x+36(0<x≤6);
(2)∵S=x2-6x+36=(x-3)2+27,1>0,
∴当x=3时,S最小;
即经过3s时,△PQD的面积最小.
点评 本题考查了矩形的性质、二次函数的最值;间接求出三角形的面积是解决问题的关键.


科目:初中数学 来源: 题型:解答题
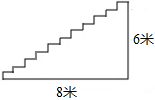 如图,凯瑞酒店准备进行装修,把楼梯铺上地毯.已知楼梯的宽度是2米,楼梯的总长度为8米,总高度为6米,已知这种地毯每平方米的售价是60元.请你帮老板算下,购买地毯多少钱?
如图,凯瑞酒店准备进行装修,把楼梯铺上地毯.已知楼梯的宽度是2米,楼梯的总长度为8米,总高度为6米,已知这种地毯每平方米的售价是60元.请你帮老板算下,购买地毯多少钱?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,A(1,4),B(3,1)
如图,平面直角坐标系中,A(1,4),B(3,1)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com