
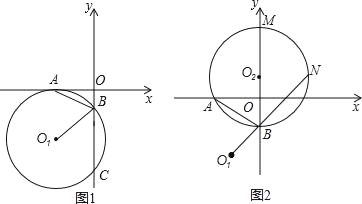
【题目】如图1在平面直角坐标系中,⊙O1与x轴切于A(﹣3,0)与y轴交于B、C两点,BC=8,连AB.
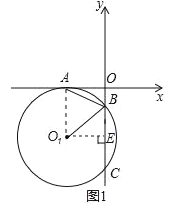
(1)求证:∠ABO1=∠ABO;
(2)求AB的长;
(3)如图2,过A、B两点作⊙O2与y轴的正半轴交于M,与O1B的延长线交于N,当⊙O2的大小变化时,得出下列两个结论:①BM﹣BN的值不变;②BM+BN的值不变.其中有且只有一个结论正确,请判断正确结论并证明.
【答案】(1)见解析;(2)![]() ;(3)①BM﹣BN的值不变,理由见解析.
;(3)①BM﹣BN的值不变,理由见解析.
【解析】
(1)连接O1A,由圆O1与x轴切于A,根据切线的性质得到O1A垂直于OA,由OB与AO垂直,根据平面内垂直于同一条直线的两直线平行,得到O1A与OB平行,根据两直线平行内错角相等,得到一对内错角相等,再由O1A=O1B,根据等边对等角可得出一对角相等,等量代换可得出∠ABO1=∠ABO,得证;
(2)作O1E⊥BC于点E,根据垂径定理得到E为BC的中点,由BC的长求出BE的长,再由A的横坐标得出OA的长,即为O1E的长,在直角三角形O1BE中,根据勾股定理求出O1B的长,用OE-BE求出OB的长,在直角三角形AOB中,根据勾股定理即可求出AB的长;
(3)两个结论中,①BM-BN的值不变正确,理由为:在MB上取一点G,使MG=BN,连接AM、AN、AG、MN,由∠ABO1为四边形ABMN的外角,根据圆内接四边形的外角等于它的内对角,可得出∠ABO1=∠NMA,再由∠ABO1=∠ABO,等量代换可得出∠ABO=∠NMA,然后利用同弧所对的圆周角相等可得出∠ABO=∠ANM,等量代换可得出∠NMA=∠ANM,根据等角对等边可得出AM=AN,再由同弧所对的圆周角相等,及OM=BN,利用SAS可得出三角形AMG与三角形ABN全等,根据全等三角形的对应边相等可得出AG=AB,由AO与BG垂直,根据三线合一得到O为BG的中点,根据OB的长求出BG的长,然后BM-BN=BM-MG=BG,由BG为常数得到BM-BN的长不变,得证.
(1)连接O1A,则O1A⊥OA,又OB⊥OA,
∴O1A∥OB,
∴∠O1AB=∠ABO,
又∵O1A=O1B,
∴∠O1AB=∠O1BA,
∴∠ABO1=∠ABO;
(2)作O1E⊥BC于点E,
∴E为BC的中点,
∵BC=8,
∴![]()
∵A(﹣3,0),
∴O1E=OA=3,
在直角三角形O1BE中,
根据勾股定理得:
![]()
∴O1A=EO=5,
∴BO=5﹣4=1,
在直角三角形AOB中,
根据勾股定理得: ![]()
(3)①BM﹣BN的值不变,理由为:
证明:在MB上取一点G,使MG=BN,连接AM、AN、AG、MN,
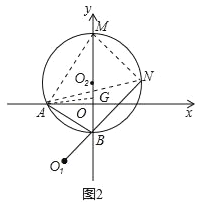
∵∠ABO1为四边形ABMN的外角,
∴∠ABO1=∠NMA,又∠ABO1=∠ABO,
∴∠ABO=∠NMA,又∠ABO=∠ANM,
∴∠AMN=∠ANM,
∴AM=AN,
∵∠AMG和∠ANB都为![]() 所对的圆周角,
所对的圆周角,
∴∠AMG=∠ANB,
在△AMG和△ANB中,
∵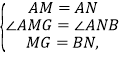
∴△AMG≌△ANB(SAS),
∴AG=AB,
∵AO⊥BG,
∴BG=2BO=2,
∴BM﹣BN=BM﹣MG=BG=2其值不变.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】在一只不透明的布袋中装有红球 3 个、黄球 1 个,这些球除颜色外都相同,均匀摇匀.
(1)从布袋中一次摸出 1 个球,计算“摸出的球恰是黄球”的概率;
(2)从布袋中一次摸出 2 个球,计算“摸出的球恰是一红一黄”的概率(用“ 画树状图”或“列表”的方法写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
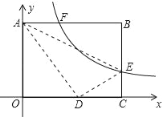
【题目】如图,将矩形ABCO放在平面直角坐标系中,其中顶点B的坐标为(5,3),E是BC边上一点,将△ABE沿AE翻折,点B刚好与OC边上的点D重合,过点E的反比例函数y=![]() 的图象与边AB交于点F,则线段AF的长为_____.
的图象与边AB交于点F,则线段AF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋数学家杨辉所著的《详解九章算法》一书中,用如图所示的三角形解释二项式![]() 的展开式中各项系数的规律,此三角形称为“杨辉三角”根据“杨辉三角”请计算
的展开式中各项系数的规律,此三角形称为“杨辉三角”根据“杨辉三角”请计算![]() 的展开式中从左起第四项的系数为( )
的展开式中从左起第四项的系数为( )

A.64B.20C.15D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
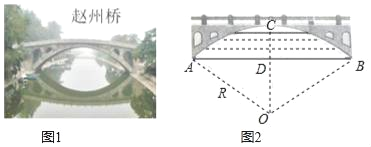
【题目】赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,
(1)如图1,尺规作图,找到桥弧所在圆的圆心O(保留作图痕迹);
(2)如图2,求桥弧AB所在圆的半径R.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下面两个定理:
①线段垂直平分线上的点到这条线段两个端点的距离相等;
②到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
应用上述定理进行如下推理:
如图,直线l是线段MN的垂直平分线.

∵点A在直线l上,∴AM=AN.( )
∵BM=BN,∴点B在直线l上.( )
∵CM≠CN,∴点C不在直线l上.
这是∵如果点C在直线l上,那么CM=CN, ( )
这与条件CM≠CN矛盾.
以上推理中各括号内应注明的理由依次是 ( )
A. ②①① B. ②①②
C. ①②② D. ①②①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,直线l为BC的中垂线,射线m为∠ABC的角平分线,直线l与m相交于点P.若∠BAC=60°,∠ACP=24°,则∠ABP的度数是( )

A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.

(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin56.3°≈0.83,cos56.3°≈0.55,tan56.3°≈1.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
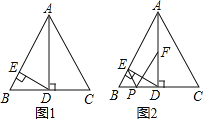
【题目】如图1,△ABC是边长为8的等边三角形,AD⊥BC下点D,DE⊥AB于点E
(1)求证:AE=3EB;
(2)若点F是AD的中点,点P是BC边上的动点,连接PE,PF,如图2所示,求PE+PF的最小值及此时BP的长;
(3)在(2)的条件下,连接EF,若AD=![]() ,当PE+PF取最小值时,△PEF的面积是 .
,当PE+PF取最小值时,△PEF的面积是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com