
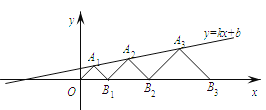
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,
,![]() ,
,![]() ,…和
,…和![]() ,
,![]() ,
,![]() ,…分别在直线
,…分别在直线![]() 和
和![]() 轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(
轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(![]() ),那么点
),那么点![]() 的纵坐标是_ _____.
的纵坐标是_ _____.
【答案】![]() .
.
【解析】
试题利用待定系数法求一次函数解析式求出直线的解析式,再求出直线与x轴、y轴的交点坐标,求出直线与x轴的夹角的正切值,分别过等腰直角三角形的直角顶点向x轴作垂线,然后根据等腰直角三角形斜边上的高线与中线重合并且等于斜边的一半,利用正切值列式依次求出三角形的斜边上的高线,即可得到各点的纵坐标的规律.
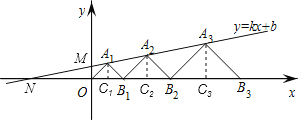
试题解析:如图:
∵A1(1,1),A2(![]() ,
,![]() )在直线y=kx+b上,
)在直线y=kx+b上,
∴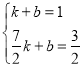 ,
,
解得![]() .
.
∴直线解析式为![]() ,
,
如图,设直线与x轴、y轴的交点坐标分别为N、M,
当x=0时,y=![]() ,
,
当y=0时,![]() ,解得x=-4,
,解得x=-4,
∴点M、N的坐标分别为M(0,![]() ),N(-4,0),
),N(-4,0),
∴tan∠MNO=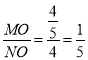 ,
,
作A1C1⊥x轴与点C1,A2C2⊥x轴与点C2,A3C3⊥x轴与点C3,
∵A1(1,1),A2(![]() ,
,![]() ),
),
∴OB2=OB1+B1B2=2×1+2×![]() =2+3=5,
=2+3=5,
tan∠MNO=![]() ,
,
∵△B2A3B3是等腰直角三角形,
∴A3C3=B2C3,
∴A3C3=![]() ,
,
同理可求,第四个等腰直角三角形A4C4=![]() ,
,
依此类推,点An的纵坐标是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边
是等边![]() 内一点,
内一点, ![]() .将
.将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() .
.

(1)求证: ![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时, ![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】身高相等的四名同学甲、乙、丙、丁参加风筝比赛,四人放出风筝的线长、线与地面的夹角如下表(假设风筝线是拉直的),则四名同学所放的风筝中最高的是( )
同学 | 甲 | 乙 | 丙 | 丁 |
放出风筝线长 | 140m | 100m | 95m | 90m |
线与地面夹角 | 30° | 45° | 45° | 60° |
A、甲B、乙
C、丙D、丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是等边△ABC边AD上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E、F分别在AC、BC上,则CE:CF=( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)求该二次函数图象与x轴的交点坐标;
(2)若m<0,当1≤x≤4时,y的最大值是2,求当1≤x≤4时,y的最小值;
(3)已知P(2,![]() ),Q(4,
),Q(4,![]() )为平面直角坐标系中两点,当抛物线与线段PQ有公共点时,请求出m的取值范围.
)为平面直角坐标系中两点,当抛物线与线段PQ有公共点时,请求出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有( )

A. 4个 B. 5个 C. 6个 D. 7个
查看答案和解析>>
科目:初中数学 来源: 题型:
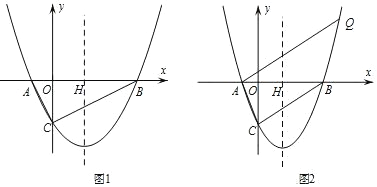
【题目】已知,抛物线 y=![]() x2+bx+c 与 y 轴交于点 C,与 x 轴交于点 A 和点B(其中点 A 在 y 轴左侧,点 B 在 y 轴右侧),对称轴直线 x=
x2+bx+c 与 y 轴交于点 C,与 x 轴交于点 A 和点B(其中点 A 在 y 轴左侧,点 B 在 y 轴右侧),对称轴直线 x=![]() 交 x 轴于点 H.
交 x 轴于点 H.
(1)若抛物线y=![]() x2+bx+c经过点(﹣4,6),求抛物线的解析式;
x2+bx+c经过点(﹣4,6),求抛物线的解析式;
(2)如图1,∠ACB=90°,点P是抛物线y=![]() x2+bx+c上位于y轴右侧的动点,且 S△ABP=S△ABC,求点 P 的坐标;
x2+bx+c上位于y轴右侧的动点,且 S△ABP=S△ABC,求点 P 的坐标;
(3)如图 2,过点A作AQ∥BC交抛物线于点Q,若点Q的纵坐标为﹣![]() c, 求点Q的坐标.
c, 求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D,AB,DC的延长线交于点E.
(1)求证:AC平分∠DAB;
(2)若BE=3,CE=3![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com