练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    下列关于抛物线和的关系说法中，正确的是（ ）
    A．它们的形状相同，开口也相同；
    B．它们都关于轴对称；
    C．它们的顶点不相同；
    D．点（，）既在抛物线上也在上
    B.
    试题分析：根据抛物线y=ax2的性质直接回答即可．
    根据两个函数知道其二次项系数a的绝对值相等，所以开口方向相反，都关于y轴对称，顶点都为原点，
    故A、C错误，B正确，
    故选B．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：解答题

    如图，在直角梯形ABCD中，∠D=∠BCD=90°，∠B=60°，AB = 6，AD = 9，点E是CD上的一个动点（E不与D重合），过点E作EF∥AC，交AD于点F（当E运动到C时，EF与AC重合），把△DEF沿着EF对折，点D的对应点是点G,如图①．

    ⑴ 求CD的长及∠1的度数；
    ⑵ 设DE = x，△GEF与梯形ABCD重叠部分的面积为y．求y与x之间的函数关系式，并求x为何值时，y的值最大?最大值是多少?
    ⑶ 当点G刚好落在线段BC上时,如图②,若此时将所得到的△EFG沿直线CB向左平移，速度为每秒1个单位，当E点移动到线段AB上时运动停止.设平移时间为t（秒）,在平移过程中是否存在某一时刻t，使得△ABE为等腰三角形?若存在，请直接写出对应的t的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，在平面直角坐标系中，已知OA=12cm，OB=6cm，点P从O点开始沿OA边向点A以1cm/s的速度移动：点Q从点B开始沿BO边向点O以1cm/s的速度移动，如果P、Q同时出发，用t(s)表示移动的时间（），那么：

    （1）设△POQ的面积为，求关于的函数解析式。
    （2）当△POQ的面积最大时，△  POQ沿直线PQ翻折后得到△PCQ，试判断点C是否落在直线AB上，并说明理由。

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，已知在平面直角坐标系中，四边形ABCO是梯形，且BC∥AO，其中A（6，0），B（3，），∠AOC=60°，动点P从点O以每秒2个单位的速度向点A运动，动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动，当点P到达A点时，点Q也随之停止，设点P，Q运动的时间为t（秒）．

    （1）求点C的坐标及梯形ABCO的面积；
    （2）当点Q在CO边上运动时，求△OPQ的面积S与运动时间t的函数关系式，并写出自变量t的取值范围；
    （3）以O，P，Q为顶点的三角形能构成直角三角形吗？若能，请求出t的值；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    二次函数的图像向下平移2个单位后经过点（1，3），那么     ．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

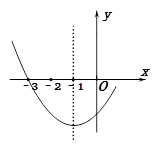
    如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=-1，且过点（-3,0）．下列说法：①abc＜0；②2a-b=0；③4a+2b+c＜0；④3a+c=0；则其中说法正确的是（　　）．
    A．①②B．②③C．①②④D．②③④

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    二次函数的顶点坐标是（ 　 ）
    A．（1，-2）B．（1，2）
    C．（0，-2）D．（0，2）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    如图为二次函数y=ax2+bx+c的图象，则下列说法中错误的是（　　）
    A．ac＜0B．2a+b=0
    C．4a+2b+c＞0D．对于任意x均有ax2+bx≥a+b

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    如图是二次函数y=ax2+bx+c（a≠0）的图象，则下列说法中正确的是（）
    A．A＞0B．4a+b＞0C．c="0"D．A+b+c＞0

    查看答案和解析>>

    同步练习册答案