
【题目】如图,在□ABCD中,以点A为圆心,以任意长为半径画圆弧,分别交边AD、AB于点M、N,再分别以点M、N为圆心,以大于![]() 长为半径画圆弧,两弧交于点P,作射线AP交边CD于点E,过点E作EF∥AD交AB于点F.若AB=5,CE=2,则四边形ADEF的周长为______.
长为半径画圆弧,两弧交于点P,作射线AP交边CD于点E,过点E作EF∥AD交AB于点F.若AB=5,CE=2,则四边形ADEF的周长为______.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在弧![]() 上.
上.
(1)求∠E的度数;
(2)连接OD、OE,当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)点G抛物线上的动点,在x轴上是否存在点E,使B、D、E、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的E点坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国东汉初年编订的一部数学经典著作在它的“方程”一章里,一次方程组是由算筹布置而成的《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2图中各行从左到右列出的算筹数分别表示未知数![]() 的系数与相应的常数项把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是
的系数与相应的常数项把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是![]() 类似地,图2所示的算筹图我们可以表述为( )
类似地,图2所示的算筹图我们可以表述为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:

(说明:成绩80分及以上为优秀,![]() 分为良好,
分为良好,![]() 分为合格,60分以下为不合格)
分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:70707071727373737475767778
这一组的是:70707071727373737475767778
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分(单位:分) | 中位数(单位:分) | 众数(单位:分) |
甲 | 74.2 |
| 85 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)上表中n的值为_____.
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是___校的学生(填“甲”或“乙”),请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0, ![]() )三点.
)三点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料题
点A、B在数轴上分别表示实数![]() 、
、![]() ,A、B两点之间的距离记作AB. 当A、B两点中有一点为原点时,不妨设A点在原点。如下图①所示,则AB =OB =
,A、B两点之间的距离记作AB. 当A、B两点中有一点为原点时,不妨设A点在原点。如下图①所示,则AB =OB =![]() =
=![]() .
.
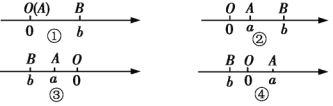
当A、B两点都不在原点时:
(1)上图②所示,点A、B都在原点的右边,不妨设点A在点B的左侧,则AB=OB-OA=![]() =
=![]() =
=![]() =
=![]()
(2)上图③所示,点A、B都在原点的左边,不妨设点A在点B的右侧,则AB=OB-OA=![]() =
=![]() =
=![]() =
=![]()
(3)如上图④所示,点A、B分别在原点的两边,不妨设点A在点O的右侧,则AB=OB+OA=![]() =
=![]() =
=![]()
回答下列问题:
①综上所述,数轴上A、B两点之间的距离AB= .
②数轴上表示2和![]() 的两点A和B之间的距离AB= .
的两点A和B之间的距离AB= .
③数轴上表示x和![]() 的两点A和B之间的距离AB= ,如果AB=2,则x的值为 .
的两点A和B之间的距离AB= ,如果AB=2,则x的值为 .
④若代数式![]() 有最小值,则最小值为 .
有最小值,则最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边![]() 的边长为
的边长为![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动,点
运动,点![]() 从点
从点![]() 出发沿
出发沿![]() 的延长线
的延长线![]() 向右运动,已知点
向右运动,已知点![]() ,
,![]() 都以
都以![]() 的速度同时开始运动,运动过程中
的速度同时开始运动,运动过程中![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 运动到点
运动到点![]() 后两点同时停止运动.
后两点同时停止运动.
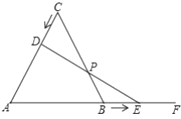
(1)当![]() 是直角三角形时,求
是直角三角形时,求![]() ,
,![]() 两点运动的时间;
两点运动的时间;
(2)求证:在运动过程中,点![]() 始终是线段
始终是线段![]() 的中点.
的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com