梯形的上底长3cm,下底长6cm,一腰长4cm.
(1)求另一腰的取值范围;
(2)选一个你认为合适的正整数作为另一腰的长,尺规作出这个梯形.
【答案】
分析:(1)过D作DE∥AB交BC于E,得到平行四边形ABED,求出DE、CE的长,在△DEC中,根据三角形的三边关系定理,即可得出结论;(2)类比(1)的辅助线先作△DEC,再作?ABED,如图,即可得到梯形ABCD.
解答: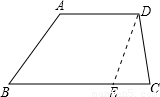
解:(1)过D作DE∥AB交BC于E,
∵AD∥BC,
∴四边形ABED是平行四边形,
∴AD=BE=3,AB=DE=4,
∴CE=6-3=3
设DC=x,
在△DEC中:4-3<x<4+3
∴1<x<7,
答:另一腰的取值范围是1<x<7
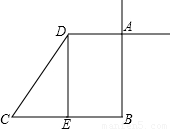
(2)取x=5,①作△DCE,使DC=5,DE=4,CE=3,
②延长CE到B使BE=3,
③分别过B、D作DE、BE的平行线,两线交于A,
则四边形ABCD为所求.
点评:本题主要考查了梯形的性质,平行四边形的性质和判定,三角形的三边关系定理等知识点,解此题的关键是把梯形转化成平行四边形和三角形.

 解:(1)过D作DE∥AB交BC于E,
解:(1)过D作DE∥AB交BC于E,

