
【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;最大值是多少?
【答案】(1)w=-10x2+700x-10000;(2)当单价为35元时,该文具每天的利润最大;最大值为2250.
【解析】
试题(1)因为销售单价![]() 元,所以根据当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.可表示出销售量=250-10(x-25)件,然后根据每天所得的销售利润
元,所以根据当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.可表示出销售量=250-10(x-25)件,然后根据每天所得的销售利润![]() (元)=一件的利润×销售量,代入化简即可;
(元)=一件的利润×销售量,代入化简即可;
(2)利用二次函数的性质,将(1)中的函数关系式配方即可得出结论.
试题解析:(1)由题意得,销售量=250-10(x-25)=-10x+500,
则w=(x-20)(-10x+500)
=-10x2+700x-10000;
(2)w=-10x2+700x-10000=-10(x-35)2+2250.
故当单价为35元时,该文具每天的利润最大;最大值为2250 10分


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】等边![]() 的边长为
的边长为![]() ,等边
,等边![]() 的边长为
的边长为![]() ,把
,把![]() 放在
放在![]() 中,使
中,使![]() 与
与![]() 重合,点
重合,点![]() 在
在![]() 边上,如图所示,此时点
边上,如图所示,此时点![]() 是
是![]() 中点,在
中点,在![]() 内部将
内部将![]() 按下列方式旋转:绕点
按下列方式旋转:绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 与点
与点![]() 重合,完成第
重合,完成第![]() 次操作,此时点
次操作,此时点![]() 是
是![]() 中点,
中点,![]() 旋转了__________
旋转了__________![]() ;再绕点
;再绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 与点
与点![]() 重合,完成第
重合,完成第![]() 次操作;……这样依次绕
次操作;……这样依次绕![]() 的某个顶点连续旋转下去,第
的某个顶点连续旋转下去,第![]() 次操作完成时,
次操作完成时,![]() _____________.
_____________.
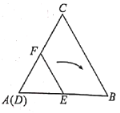
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九“勾股”章,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”译文:“如图,今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)你的计算结果是:出南门________步而见木.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.求证:BD是四边形ABCD的“相似对角线”.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
已知实数m,n满足(2m3+n3+1)(2m3+n3-1)=80,试求2m3+n3的值
解:设2m3+n3=t,则原方程变为(t+1)(t-1)=80,整理得t2-1=80,t2=81, t=±9,所以2m3+n3=±9
上面这种方法称为“换元法”,把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂的问题简单化.
根据以上阅读材料内容,解决下列问题,并写出解答过程.
已知实数x,y满足(4x2+4y2+3)(4x2+4y2-3)=27,求x2+y2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣3,﹣2,﹣1,0,1,2,3这七个数中,随机抽取一个数记为m,若数m使关于x的分式方程![]() ﹣1=
﹣1=![]() 的解是非负数,且使得二次函数y=(m﹣2)x2+2x+1的图象与x轴有交点,那么满足条件所有m之和是( )
的解是非负数,且使得二次函数y=(m﹣2)x2+2x+1的图象与x轴有交点,那么满足条件所有m之和是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数![]() (k为常数,k ≠0)的图象上,正方形ADEF的面积为16,且BF=2AF,则k值为
(k为常数,k ≠0)的图象上,正方形ADEF的面积为16,且BF=2AF,则k值为
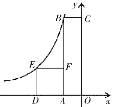
A.-8B.-12C.-24D.-36
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日贵州环保行活动“美丽乌江 拒绝污染”正式开启,乌江支流由于长期采磷及磷化工发展造成了总磷污染.当地政府提出五条整改措施,力求在
日贵州环保行活动“美丽乌江 拒绝污染”正式开启,乌江支流由于长期采磷及磷化工发展造成了总磷污染.当地政府提出五条整改措施,力求在![]() 天以内使总磷含量达标(即总磷浓度低于
天以内使总磷含量达标(即总磷浓度低于![]() ).整改过程中,总磷浓度
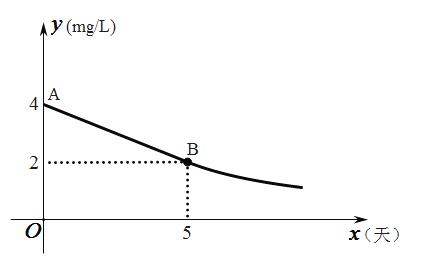
).整改过程中,总磷浓度![]() 与时间
与时间![]() (天)的变化规律如图所示,其中线段
(天)的变化规律如图所示,其中线段![]() 表示前
表示前![]() 天的变化规律,且线段
天的变化规律,且线段![]() 所在直线的表达式为:
所在直线的表达式为:![]() ,从第
,从第![]() 天起,该支流总磷浓度
天起,该支流总磷浓度![]() 与时间
与时间![]() 成反比例关系.
成反比例关系.
(1)求整改全过程中总磷浓度![]() 与时间
与时间![]() 的函数表达式;
的函数表达式;
(2)该支流中总磷的浓度能否在![]() 天以内达标?说明理由.
天以内达标?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以矩形ABCD的边CD为直径作⊙O,点E是AB 的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H.

(1)若连接AO,试判断四边形AECO的形状,并说明理由;
(2)求证:AH是⊙O的切线;
(3)若AB=6,CH=2,则AH的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com