
分析 根据方程组的解的定义,$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$应满足方程②,$\left\{\begin{array}{l}{x=5}\\{y=4}\end{array}\right.$应满足方程①,将它们分别代入方程②①,就可得到关于a,b的二元一次方程组,解得a,b的值,即可解答.
解答 解:∵甲看错了方程①中的a,得到方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$,
∴-12+b=-2,
解得:b=10,
∵乙看错了方程②中的b,得到方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=4}\end{array}\right.$,
∴5a+20=15,
解得:a=-1,
则a2012+(-$\frac{1}{10}$b)2013=$(-1)^{2012}+(-\frac{1}{10}×10)^{2013}$=1+(-1)=0.
点评 此题主要考查了二元一次方程组解的定义,以及解二元一次方程组的基本方法,解决本题的关键是熟记二元一次方程组的解.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
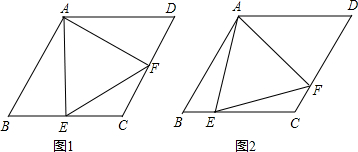
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
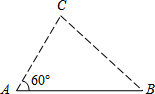 小彬和小红分别在平坦的冰面上的点A和点B处.如图,点A和点B之间的距离是100米,小彬离开点A以每秒8米的速度沿着与AB成60°角的直线滑行,在小彬离开点A的同时,小红以每秒7米的速度也沿着一条直线滑行离开点B,这条直线能使小彬与小红以所给的速度最早相遇的时间是多少秒?
小彬和小红分别在平坦的冰面上的点A和点B处.如图,点A和点B之间的距离是100米,小彬离开点A以每秒8米的速度沿着与AB成60°角的直线滑行,在小彬离开点A的同时,小红以每秒7米的速度也沿着一条直线滑行离开点B,这条直线能使小彬与小红以所给的速度最早相遇的时间是多少秒?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com