
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 全等三角形的对应边相等,对应角相等,
对应边上的对应高相等,对应中线相等,对应角平分线相等.
不是对应边上的高线,中线就不一定相等.
不是对应角的平分线也不一定相等.
解答 解:∵在△ABC和△A′B′C′中,
$\left\{\begin{array}{l}{∠A=∠{A}^{′}}\\{AB={A}^{′}{B}^{′}}\\{∠C=∠{C}^{′}}\end{array}\right.$
∴△ABC≌△A′C′B′
∴∠B=∠B′;∠B的平分线与∠B′的平分线相等;BC边上的高与B′C′边上的高相等;BC边上的中线与B′C′边上的中线相等,
正确的有(1)(2)(3)(4),
故选:D.
点评 本题考查了全等三角形性质的应用;容易出现的错误是:受字母的影响,找错对应角,与对应顶点,正确确定对应关系是解题的关键.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED的边长,已知AE=$\sqrt{2}$c,这时我们把关于x的形如ax2+$\sqrt{2}$cx+b=0的一元二次方程称为“勾系一元二次方程”.
如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED的边长,已知AE=$\sqrt{2}$c,这时我们把关于x的形如ax2+$\sqrt{2}$cx+b=0的一元二次方程称为“勾系一元二次方程”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
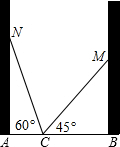 如图,在一个房间内,有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MB=m米,梯子的倾斜角度∠MCB=45°.若梯子斜靠在对面墙上,梯子的倾斜角度∠NCA=60°.试求该房间的宽和梯子的长度.
如图,在一个房间内,有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MB=m米,梯子的倾斜角度∠MCB=45°.若梯子斜靠在对面墙上,梯子的倾斜角度∠NCA=60°.试求该房间的宽和梯子的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com