
分析 (1)利用公式法或配方法解方程即可;
(2)设这个方程的根为x1、x2,即当x=x1,x=x2时,y=4,可设抛物线解析式y=a(2x2-x-8)+4,再将x=2,y=-4代入求a即可.
解答 解:
(1)∵2x2-x-8=0,
∴a=2,b=-1c=-8,
∴△=1+64=65>0,
∴x1=$\frac{1+\sqrt{65}}{4}$,x2=$\frac{1-\sqrt{65}}{4}$;
(2)设方程2x2-x-8=0的根为x1、x2,则
当x=x1,x=x2时,y=4,可设y=a(2x2-x-8)+4,
把x=2,y=-4代入,得-4=a(2×22-2-8)+4,
解得a=4,
所求函数为y=4(2x2-x-8)+4,
即y=8x2-4x-28.
点评 本题综合考查了一元二次方程的根与二次函数图象上点的坐标的关系,巧妙地设二次函数解析式,用待定系数法求解析式.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:解答题
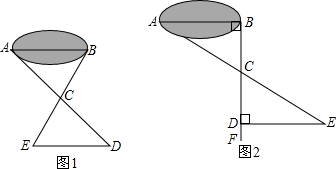 八(3)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
八(3)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,是2016年11月月历:
如图,是2016年11月月历:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com