
【题目】在等边△ABC外侧作直线AP,点B关于直线AP的对称点为D,连接BD,CD,其中CD交直线AP于点E. 
(1)依题意补全图1;
(2)若∠PAB=30°,求∠ACE的度数;
(3)如图2,若60°<∠PAB<120°,判断由线段AB,CE,ED可以构成一个含有多少度角的三角形,并证明. 
【答案】
(1)解:所作图形如图1所示:

(2)解:连接AD,如图1.
∵点D与点B关于直线AP对称,
∴AD=AB,∠DAP=∠BAP=30°,
∵AB=AC,∠BAC=60°,
∴AD=AC,∠DAC=120°,
∴2∠ACE+60°+60°=180°,
∴∠ACE=30°

(3)解:线段AB,CE,ED可以构成一个含有60°角的三角形.
证明:连接AD,EB,如图2.
∵点D与点B关于直线AP对称,
∴AD=AB,DE=BE,
∴∠EDA=∠EBA,
∵AB=AC,AB=AD,
∴AD=AC,
∴∠ADE=∠ACE,
∴∠ABE=∠ACE.
设AC,BE交于点F,
又∵∠AFB=∠CFE,
∴∠BAC=∠BEC=60°,
∴线段AB,CE,ED可以构成一个含有60°角的三角形.

【解析】(1)根据题意作出图形;(2)根据题意可得∠DAP=∠BAP=30°,然后根据AB=AC,∠BAC=60°,得出AD=AC,∠DAC=120°,最后根据三角形的内角和公式求解;(3)由线段AB,CE,ED可以构成一个含有60度角的三角形,连接AD,EB,根据对称可得∠EDA=∠EBA,然后证得AD=AC,最后即可得出∠BAC=∠BEC=60°.


科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且AE=BD,
(1)当点E为AB的中点时,如图1,求证:EC=ED; 
(2)当点E不是AB的中点时,如图2,过点E作EF∥BC,求证:△AEF是等边三角形; 
(3)在第(2)小题的条件下,EC与ED还相等吗,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的横坐标为﹣1,点B在x轴的负半轴上,AB=AO,∠ABO=30°,直线MN经过原点O,点A关于直线MN的对称点A1在x轴的正半轴上,点B关于直线MN的对称点为B1 , 则∠AOM的度数为;点B1的纵坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平行四边形ABCD中,下列结论不一定正确的是( )
A. AB﹦CD B. 当AC⊥BD时,它是菱形
C. AC﹦BD D. 当∠ABC﹦90°时,它是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
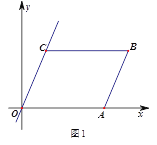
【题目】如图,在平面直角坐标系中,四边形OABC是平行四边形.直线L经过O、C两点.点A的坐标为(8,0),点B的坐标为(11,4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C﹣B相交于点M.当Q、M两点相遇时,P、Q两点停止运动,设点P、Q运动的时间为t秒(t>0).△MPQ的面积为S.
(1)点C的坐标为 ,直线L的解析式为 .
(2)试求点Q与点M相遇前S与t的函数关系式,并写出相应的t的取值范围.
(3)试求题(2)中当t为何值时,S的值最大,并求出S的最大值.
(4)随着P、Q两点的运动,当点M在线段CB上运动时,设PM的延长线与直线L相交于点N.试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算。
(1)解方程: ![]() =1﹣
=1﹣ ![]()
(2)先化简,再求值: ![]() (9ab2﹣3)+(7a2b﹣2)+2(ab2+1)﹣2a2b,其中a、b满足(a+2)2+|b﹣3|=0.
(9ab2﹣3)+(7a2b﹣2)+2(ab2+1)﹣2a2b,其中a、b满足(a+2)2+|b﹣3|=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用两个全等的直角三角形拼下列图形:①平行四边形(不包含菱形、矩形、正方形);②矩形;③菱形;④正方形;⑤等腰三角形.一定可以拼成的图形是_____________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B都在数轴上,且AB=6 ![]()
(1)点B表示的数是;
(2)若点B以每秒2个单位的速度沿数轴向右运动,则2秒后点B表示的数是;
(3)若点A、B都以每秒2个单位沿数轴向右运动,而点O不动,t秒后有一个点是一条线段的中点,求t.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com