
【题目】在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于点A(﹣1,0)、点B,与y轴交于点C,抛物线的对称轴是直线x=1,连接BC、AC.
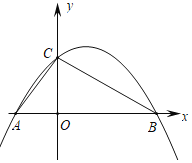
(1)求S△ABC(用含有a的代数式来表示);
(2)若S△ABC=6,求抛物线的解析式;
(3)在(2)的条件下,当﹣1≤x≤m+1时,y的最大值是2,求m的值.
【答案】(1)﹣6a;(2)y=﹣x2+2x+3;(3)m=﹣![]() .
.
【解析】
(1)利用A(﹣1,0),对称轴是直线x=1,用含a的式子表示函数解析式,再求出点B的坐标即可求出S△ABC;
(2)将S△ABC=6代入求出a,即可得到抛物线的解析式;
(3)分两种情况讨论:①当m+1≤1时,即m≤0,②当m>0时,分别代入解析式求出m的值.
(1)将点A的坐标代入抛物线表达式得:a﹣b+c=0…①,
函数的对称轴为:x=1=﹣![]() …②,
…②,
联立①②并解得:b=﹣2a,c=﹣3a,
故抛物线的表达式为:y=ax2﹣2ax﹣3a,
则点B的坐标为:(3,0);
S△ABC=![]() AB×OC=
AB×OC=![]() 4×(﹣3a)=﹣6a;
4×(﹣3a)=﹣6a;
(2)S△ABC=﹣6a=6,解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+2x+3;
(3)①当m+1≤1时,即m≤0,
函数在x=m+1时,取得最大值,
即:﹣(m+1)2+2(m+1)+3=2,
解得:m=![]() (舍去正值),
(舍去正值),
故m=﹣![]() ;
;
②当m>0时,函数在顶点处取得最大值,而顶点纵坐标为4≠2,
故不存在m值;
综上,m=﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】 如图,等边△ABC中,点D是BC上任一点,以AD为边作∠ADE=∠ADF=60°,分别交AC,AB于点E,F.
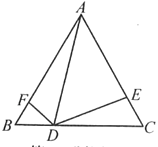
(1)求证:AD2=AEAC.
(2)已知BC=2,设BD的长为x,AF的长为y.
①求y关于x的函数表达式;
②若四边形AFDE外接圆直径为![]() ,求x的值
,求x的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D,AB,DC的延长线交于点E.
(1)求证:AC平分∠DAB;
(2)若BE=3,CE=3![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“优秀传统文化进校园”活动中,学校计划每周二下午第三节课时间开展此项活动,拟开展活动项目为:剪纸,武术,书法,器乐,要求七年级学生人人参加,并且每人只能参加其中一项活动.教务处在该校七年级学生中随机抽取了100名学生进行调查,并对此进行统计,绘制了如图所示的条形统计图和扇形统计图(均不完整).

请解答下列问题:
(1)请补全条形统计图和扇形统计图;
(2)在参加“剪纸”活动项目的学生中,男生所占的百分比是多少?
(3)若该校七年级学生共有500人,请估计其中参加“书法”项目活动的有多少人?
(4)学校教务处要从这些被调查的女生中,随机抽取一人了解具体情况,那么正好抽到参加“器乐”活动项目的女生的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解七年级学生最喜欢的学科,从七年级学生中随机抽取部分学生进行“我最喜欢的学科(语文、数学、外语)”试卷调查,请根据两幅统计图中的信息回答下列问题:

(1)本次抽样调查共抽取了 名学生;最喜欢“外语”的学生有 人;
(2)如果该学校七年级有500人,那么最喜欢外语学科的人数大概有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2﹣2x+3.问:
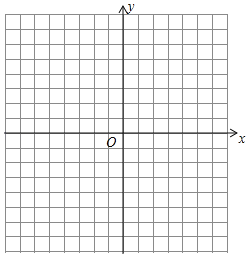
(1)该抛物线的顶点坐标是 ;
(2)该函数与x轴的交点坐标是 , ,并在网格中画出该函数的图象;
(3)x取什么值时,抛物线在x轴上方? .
(4)已知y=t,t取什么值时与抛物线y=﹣x2﹣2x+3有两个交点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是边长为2的正方形ABCD的边BC上的一动点(不与端点重合),将△ABE沿AE翻折至△AFE的位置,若△CDF是等腰三角形,则BE=________.
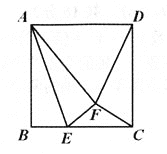
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别写有数字﹣1,1,2的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后.
(1)随机抽取一张,求抽到数字2的概率;
(2)随机抽取一张,以其正面数字作为a的值,然后再从剩余的两张卡片随机抽一张,以其正面的数字作为b的值,请你用画树状图或列表格的方法表示所有可能的结果,并求出点(a,b)在第四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):
运动员 \ 环数 \ 次数 | 1 | 2 | 3 | 4 | 5 |
甲 | 10 | 8 | 9 | 10 | 8 |
乙 | 10 | 9 | 9 | a | b |
某同学计算出了甲的成绩平均数是9,方差是![]() =
=![]() [(10-9)2+(8-9)2+(9-9)2+(10-9)2+(8-9)2]=0.8,
[(10-9)2+(8-9)2+(9-9)2+(10-9)2+(8-9)2]=0.8,
请作答:
(1)若甲、乙射击成绩平均数都一样,则a+b= ;
(2)在(1)的条件下,当甲比乙的成绩较稳定时,请列举出a,b的所有可能取值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com