
ЁОЬтФПЁПЃЈЮЪЬтГЪЯжЃЉАЂЛљУзЕТелЯвЖЈРэЃК
ШчЭМ1ЃЌABКЭBCЪЧЁбOЕФСНЬѕЯвЃЈМДелЯпABCЪЧдВЕФвЛЬѕелЯвЃЉЃЌBCЃОABЃЌЕуMЪЧ![]() ЕФжаЕуЃЌдђДгMЯђBCЫљзїДЙЯпЕФДЙзуDЪЧелЯвABCЕФжаЕуЃЌМДCDЃНDB+BAЃЎЯТУцЪЧдЫгУЁАНиГЄЗЈЁБжЄУїCDЃНDB+BAЕФВПЗжжЄУїЙ§ГЬЃЎ
ЕФжаЕуЃЌдђДгMЯђBCЫљзїДЙЯпЕФДЙзуDЪЧелЯвABCЕФжаЕуЃЌМДCDЃНDB+BAЃЎЯТУцЪЧдЫгУЁАНиГЄЗЈЁБжЄУїCDЃНDB+BAЕФВПЗжжЄУїЙ§ГЬЃЎ
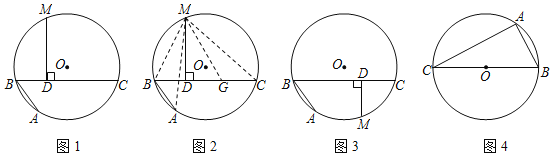
жЄУїЃКШчЭМ2ЃЌдкCDЩЯНиШЁCGЃНABЃЌСЌНгMAЁЂMBЁЂMCКЭMGЃЎ
ЁпMЪЧ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ
ЁрMAЃНMCЂй
гжЁпЁЯAЃНЁЯCЂк
ЁрЁїMABЁеЁїMCGЂл
ЁрMBЃНMG
гжЁпMDЁЭBC
ЁрBDЃНDG
ЁрAB+BDЃНCG+DG
МДCDЃНDB+BA
ИљОнжЄУїЙ§ГЬЃЌЗжБ№аДГіЯТСаВНжшЕФРэгЩЃК
ЂйЁЁ ЁЁЃЌ
ЂкЁЁ ЁЁЃЌ
ЂлЁЁ ЁЁЃЛ
ЃЈРэНтдЫгУЃЉШчЭМ1ЃЌABЁЂBCЪЧЁбOЕФСНЬѕЯвЃЌABЃН4ЃЌBCЃН6ЃЌЕуMЪЧ![]() ЕФжаЕуЃЌMDЁЭBCгкЕуDЃЌдђBDЃНЁЁ ЁЁЃЛ
ЕФжаЕуЃЌMDЁЭBCгкЕуDЃЌдђBDЃНЁЁ ЁЁЃЛ
ЃЈБфЪНЬНОПЃЉШчЭМ3ЃЌШєЕуMЪЧ![]() ЕФжаЕуЃЌЃЈЮЪЬтГЪЯжЃЉжаЕФЦфЫћЬѕМўВЛБфЃЌХаЖЯCDЁЂDBЁЂBAжЎМфДцдкдѕбљЕФЪ§СПЙиЯЕЃПВЂМгвджЄУїЃЎ
ЕФжаЕуЃЌЃЈЮЪЬтГЪЯжЃЉжаЕФЦфЫћЬѕМўВЛБфЃЌХаЖЯCDЁЂDBЁЂBAжЎМфДцдкдѕбљЕФЪ§СПЙиЯЕЃПВЂМгвджЄУїЃЎ
ЃЈЪЕМљгІгУЃЉИљОнФуЖдАЂЛљУзЕТелЯвЖЈРэЕФРэНтЭъГЩЯТСаЮЪЬтЃК
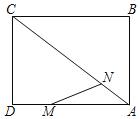
ШчЭМ4ЃЌBCЪЧЁбOЕФжБОЖЃЌЕуAдВЩЯвЛЖЈЕуЃЌЕуDдВЩЯвЛЖЏЕуЃЌЧвТњзуЁЯDACЃН45ЁуЃЌШєABЃН6ЃЌЁбOЕФАыОЖЮЊ5ЃЌЧѓADГЄЃЎ
ЁОД№АИЁПЃЈЮЪЬтГЪЯжЃЉЯрЕШЕФЛЁЫљЖдЕФЯвЯрЕШЃЛЭЌЛЁЫљЖдЕФдВжмНЧЯрЕШЃЛгаСНзщБпМАЦфМаНЧЗжБ№ЖдгІЯрЕШЕФСНИіШ§НЧаЮШЋЕШЃЛЃЈРэНтдЫгУЃЉ1ЃЛЃЈБфЪНЬНОПЃЉDBЃНCD+BAЃЛжЄУїМћНтЮіЃЛЃЈЪЕМљгІгУЃЉ7![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈЮЪЬтГЪЯжЃЉИљОндВЕФаджЪМДПЩЧѓНтЃЛ
ЃЈРэНтдЫгУЃЉCDЃНDB+BAЃЌМДCDЃН6ЉCD+ABЃЌМДCDЃН6ЉCD+4ЃЌНтЕУЃКCDЃН5ЃЌМДПЩЧѓНтЃЛ
ЃЈБфЪНЬНОПЃЉжЄУїЁїMABЁеЁїMGBЃЈSASЃЉЃЌдђMAЃНMGЃЌMCЃНMGЃЌгжDMЁЭBCЃЌдђDCЃНDGЃЌМДПЩЧѓНтЃЛ
ЃЈЪЕМљгІгУЃЉвбжЊЁЯD1ACЃН45ЁуЃЌЙ§ЕуD1зїD1G1ЁЭACгкЕуG1ЃЌдђCG1Ёф+ABЃНAG1ЃЌЫљвдAG1ЃН![]() ЃЈ6+8ЃЉЃН7ЃЎШчЭМЁЯD2ACЃН45ЁуЃЌЭЌРэвзЕУAD2ЃН
ЃЈ6+8ЃЉЃН7ЃЎШчЭМЁЯD2ACЃН45ЁуЃЌЭЌРэвзЕУAD2ЃН![]() ЃЎ
ЃЎ
ЃЈЮЪЬтГЪЯжЃЉ
ЂйЯрЕШЕФЛЁЫљЖдЕФЯвЯрЕШ
ЂкЭЌЛЁЫљЖдЕФдВжмНЧЯрЕШ
ЂлгаСНзщБпМАЦфМаНЧЗжБ№ЖдгІЯрЕШЕФСНИіШ§НЧаЮШЋЕШ
ЙЪД№АИЮЊЃКЯрЕШЕФЛЁЫљЖдЕФЯвЯрЕШЃЛЭЌЛЁЫљЖЈвхЕФдВжмНЧЯрЕШЃЛгаСНзщБпМАЦфМаНЧЗжБ№ЖдгІЯрЕШЕФСНИіШ§НЧаЮШЋЕШЃЛ
ЃЈРэНтдЫгУЃЉCDЃНDB+BAЃЌМДCDЃН6ЉCD+ABЃЌМДCDЃН6ЉCD+4ЃЌНтЕУЃКCDЃН5ЃЌ
BDЃНBCЉCDЃН6Љ5ЃН1ЃЌ
ЙЪД№АИЮЊЃК1ЃЛ
ЃЈБфЪНЬНОПЃЉDBЃНCD+BAЃЎ
жЄУїЃКдкDBЩЯНиШЅBGЃНBAЃЌСЌНгMAЁЂMBЁЂMCЁЂMGЃЌ
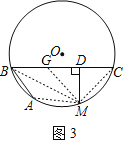
ЁпMЪЧЛЁACЕФжаЕуЃЌ
ЁрAMЃНMCЃЌЁЯMBAЃНЁЯMBGЃЎ
гжMBЃНMB
ЁрЁїMABЁеЁїMGBЃЈSASЃЉ
ЁрMAЃНMG
ЁрMCЃНMGЃЌ
гжDMЁЭBCЃЌ
ЁрDCЃНDGЃЌ
AB+DCЃНBG+DGЃЌ
МДDBЃНCD+BAЃЛ
ЃЈЪЕМљгІгУЃЉ
ШчЭМЃЌBCЪЧдВЕФжБОЖЃЌЫљвдЁЯBACЃН90ЁуЃЎ
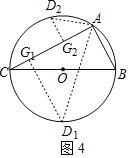
вђЮЊABЃН6ЃЌдВЕФАыОЖЮЊ5ЃЌЫљвдACЃН8ЃЎ
вбжЊЁЯD1ACЃН45ЁуЃЌЙ§ЕуD1зїD1G1ЁЭACгкЕуG1ЃЌ
дђCG1Ёф+ABЃНAG1ЃЌ
ЫљвдAG1ЃН![]() ЃЈ6+8ЃЉЃН7ЃЎ
ЃЈ6+8ЃЉЃН7ЃЎ
ЫљвдAD1ЃН7![]() ЃЎ
ЃЎ
ШчЭМЁЯD2ACЃН45ЁуЃЌЭЌРэвзЕУAD2ЃН![]() ЃЎ
ЃЎ
ЫљвдADЕФГЄЮЊ7![]() Лђ
Лђ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН6ЃЌADЃН8ЃЌЕуMЃЌNЗжБ№ЮЊADЃЌACЩЯЕФЖЏЕуЃЈВЛКЌЖЫЕуЃЉЃЌANЃНDMЃЌСЌНсЕуMгыОиаЮЕФвЛИіЖЅЕуЃЌвдИУЯпЖЮЮЊжБОЖзїЁбOЃЌЕБЕуNКЭОиаЮЕФСэвЛИіЖЅЕувВдкЁбOЩЯЪБЃЌЯпЖЮDMЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧАыОЖЮЊ1ЕФ
ЪЧАыОЖЮЊ1ЕФ![]() ЕФФкНге§ЪЎБпаЮЃЌ
ЕФФкНге§ЪЎБпаЮЃЌ![]() ЦНЗж
ЦНЗж![]()
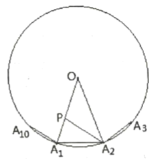
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
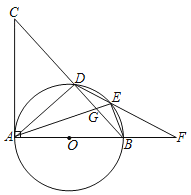
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌACЁЭABЃЌBCНЛЁбOгкЕуDЃЌЕуEдкСгЛЁBDЩЯЃЌDEЕФбгГЄЯпНЛABЕФбгГЄЯпгкЕуFЃЌСЌНгAEНЛBDгкЕуGЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯAEDЃНЁЯCADЃЛ
ЃЈ2ЃЉШєЕуEЪЧСгЛЁBDЕФжаЕуЃЌЧѓжЄЃКED2ЃНEGEAЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєBOЃНBFЃЌDEЃН2ЃЌЧѓEFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
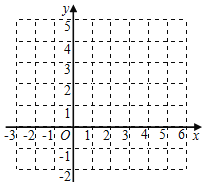
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНx2Љ4x+3ЃЎ
ЃЈ1ЃЉдкЫљИјЕФЦНУцжБНЧзјБъЯЕжаЛГіЫќЕФЭМЯѓЃЛ
ЃЈ2ЃЉШєШ§ЕуAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЌCЃЈx3ЃЎy3ЃЉЧв2ЃМx1ЃМx2ЃМx3ЃЌдђy1ЃЌy2ЃЌy3ЕФДѓаЁЙиЯЕЮЊЁЁ ЁЁЃЎ
ЃЈ3ЃЉАбЫљЛЕФЭМЯѓШчКЮЦНвЦЃЌПЩвдЕУЕНКЏЪ§yЃНx2ЕФЭМЯѓЃПЧыаДГівЛжжЦНвЦЗНАИЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
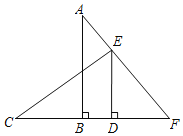
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЕуCЁЂDЁЂBЁЂFдквЛЬѕжБЯпЩЯЃЌЧвABЁЭBDЃЌDEЁЭBDЃЌABЃНCDЃЌCEЃНAFЃЎ
ЧѓжЄЃКЃЈ1ЃЉЁїABFЁеЁїCDEЃЛ
ЃЈ2ЃЉCEЁЭAFЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвх:Ш§НЧаЮвЛБпЩЯЕФЕуНЋИУБпЗжЮЊСНЬѕЯпЖЮЃЌЧветСНЬѕЯпЖЮЕФЛ§ЕШгкетИіЕуЕНИУБпЫљЖдЖЅЕуСЌЯпЕФЦНЗНЃЌдђГЦетИіЕуЮЊШ§НЧаЮИУБпЕФЁАКУЕуЁБ.ШчЭМ1ЃЌЁїABCжаЃЌЕуDЪЧBCБпЩЯвЛЕуЃЌСЌНсADЃЌШє![]() ЃЌдђГЦЕуDЪЧЁїABCжаBCБпЩЯЕФЁАКУЕуЁБ.
ЃЌдђГЦЕуDЪЧЁїABCжаBCБпЩЯЕФЁАКУЕуЁБ.
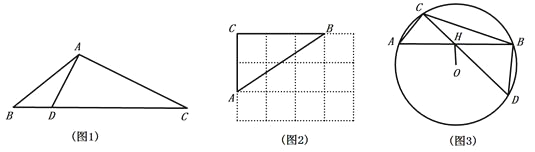
ЃЈ1ЃЉШчЭМ2ЃЌЁїABCЕФЖЅЕуЪЧ![]() ЭјИёЭМЕФИёЕуЃЌЧыНігУжБГпЛГіABБпЩЯЕФвЛИіЁАКУЕуЁБ.
ЭјИёЭМЕФИёЕуЃЌЧыНігУжБГпЛГіABБпЩЯЕФвЛИіЁАКУЕуЁБ.
ЃЈ2ЃЉЁїABCжаЃЌBC=9ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕуDЪЧBCБпЩЯЕФЁАКУЕуЁБЃЌЧѓЯпЖЮBDЕФГЄ.
ЃЌЕуDЪЧBCБпЩЯЕФЁАКУЕуЁБЃЌЧѓЯпЖЮBDЕФГЄ.
ЃЈ3ЃЉШчЭМ3ЃЌЁїABCЪЧ![]() ЕФФкНгШ§НЧаЮЃЌOHЁЭABгкЕуHЃЌСЌНсCHВЂбгГЄНЛ
ЕФФкНгШ§НЧаЮЃЌOHЁЭABгкЕуHЃЌСЌНсCHВЂбгГЄНЛ![]() гкЕуD.
гкЕуD.
ЂйЧѓжЄЃКЕуHЪЧЁїBCDжаCDБпЩЯЕФЁАКУЕуЁБ.
ЂкШє![]() ЕФАыОЖЮЊ9ЃЌЁЯABD=90ЁуЃЌOH=6ЃЌЧыжБНгаДГі
ЕФАыОЖЮЊ9ЃЌЁЯABD=90ЁуЃЌOH=6ЃЌЧыжБНгаДГі![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
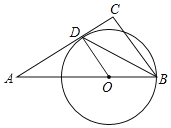
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌOЪЧABБпЩЯЕФЕуЃЌвдOЮЊдВаФЃЌOBЮЊАыОЖЕФЁб0гыACЯрЧагкЕуDЃЌBDЦНЗжЁЯABCЃЌADЃН![]() ODЃЌABЃН12ЃЌЧѓCDЕФГЄЃЎ
ODЃЌABЃН12ЃЌЧѓCDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГОАЧјФкгавЛПщОиаЮгЭВЫЛЈЬяЕиЃЈЪ§ОнШчЭМЪОЃЌЕЅЮЛЃКm.ЃЉЯждкЦфжааоНЈвЛЬѕЙлЛЈЕРЃЈЭМжавѕгАВПЗжЃЉЙЉгЮШЫЩЭЛЈ.ЩшИФдьКѓЪЃгргЭВЫЛЈЕиЫљеМУцЛ§ЮЊym2.
ЃЈ1ЃЉЧѓyгыxЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШєИФдьКѓЙлЛЈЕРЕФУцЛ§ЮЊ13m2ЃЌЧѓxЕФжЕЃЛ
ЃЈ3ЃЉШєвЊЧѓ 0.5Ём x Ём1ЃЌЧѓИФдьКѓЪЃгргЭВЫЛЈЕиЫљеМУцЛ§ЕФзюДѓжЕ.

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com