Question

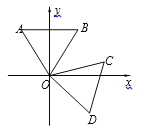
【题目】如图，点O是直线AB上的一点，OC平分∠AOB，在直线AB另一端以O为顶点作∠DOE=900。

（1） 若∠AOE=480，求∠BOD的度数。

（2） 写出图中与∠AOE互余的角。

（3） ∠AOE与∠COD有什么数量关系，请写出你的结论并说明理由。

Answer 1

【答案】（1）∠BOD=42°；（2）∠BOD；（3）∠AOE+∠COD=180°.

【解析】

（1）∠BOD=180°-∠AOE-DOE=42°；
（2）由∠AOE+∠BOD=90°，得出与∠AOE互余的角是∠BOD；
（3）先求出∠BOC=90°，再由∠AOE+∠BOD=90°，得出∠AOE+∠COD=180°．

（1）∵∠AOE=48°，∠DOE=90°，
∴∠BOD=180°-90°-48°=42°；
（2）∵∠DOE=90°，
∴∠AOE+∠BOD=180°-90°=90°，
∴∠BOD与∠AOE互余，
∴图中与∠AOE互余的角是∠BOD；
（3）∠AOE+∠COD=180°；理由如下：
∵OC平分∠AOB，
∴∠AOC=∠BOC=90°，
∵∠AOB=180°，∠DOE=90°，
∴∠AOE+∠BOD=90°，
∴∠AOE+∠COD=∠AOE+∠BOD+∠BOC=90°+90°=180°．