
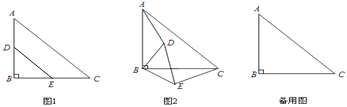
【题目】如图1,△DBE和△ABC都是等腰直角三角形,D,E两点分别在AB,BC上,∠B=90°.将△DBE绕点B顺时针旋转,得到图2.
(1)在图2中,求证:AD=CE;
(2)设AB= ![]() ,BD=
,BD= ![]() ,且当A、D、E三点在同一直线上时,∠EAC=30°,请利用备用图画出此情况下的图形,并求旋转的角度和
,且当A、D、E三点在同一直线上时,∠EAC=30°,请利用备用图画出此情况下的图形,并求旋转的角度和![]() 的值.
的值.
【答案】(1)详见解析;(2)30°,![]() .
.
【解析】试题分析:由△DBE和△ABC都是等腰直角三角形,可得AB=BC, DB=BE,∠ABD=∠CBE,根据“SAS”可证△ABD≌△CBE,从而AD=CE;
(2)先证△ABD≌△CBE,可求∠ADB=∠CEB=135°,可求∠AEC=90°,进而求出∠BAD=45°-30°=15°,根据三角形内角和即可旋转角∠ABD的度数;由AE=AD+DE=cos30 ·AC,整理可得![]() 的值.
的值.
解:(1)∵△DBE和△ABC都是等腰直角三角形,
∴AB=BC, DB=BE,∠ABC=∠DBE=90°,∴∠ABD=90°-∠DBC=∠CBE=90°-∠DBC,
∴△ABD≌△CBE,
∴AD=CE;
(2)如图, A、D、E三点在同一直线上时,

∵△DBE和△ABC都是等腰直角三角形,
∴∠BAC=∠BDE=∠BED =45°,
又△ABD≌△CBE,∴∠ADB=∠CEB=135°.
∴∠AEC=90°,
∵∠EAC=30°,
∴∠BAD=45°-30°=15°,∴∠ABD=30°,即旋转角为30°.
∵△DBE和△ABC是等腰直角三角形,AB=![]() , BD=
, BD=![]() ,
,
∴AC=![]() ,DE=
,DE=![]() ,
,
∵△ABD≌△CBE,
∴AD=EC,
∵∠EAC=30°,∠AEC=90°,AC= ![]() ,
,
∴AD=EC=![]() ,
,
∴AE=AD+DE=![]() +
+![]() =
=![]() ,
,
整理得![]() .
.


科目:初中数学 来源: 题型:
【题目】甲、乙两人共同计算一道整式:(x+a)(2x+b),由于甲抄错了a的符号,得到的结果是2x2-7x+3,乙漏抄了第二个多项式中x的系数,得到的结果是x2+2x-3.
(1)求a,b的值;(2)请计算这道题的正确结果
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对数轴上的点![]() 进行如下操作:先把点
进行如下操作:先把点![]() 表示的数乘以
表示的数乘以![]() ,再把所得数对应的点沿数轴向右平移
,再把所得数对应的点沿数轴向右平移![]() 个单位长度,得到点
个单位长度,得到点![]() .称这样的操作为点
.称这样的操作为点![]() 的“倍移”,对数轴上的点
的“倍移”,对数轴上的点![]() ,
,![]() ,
, ![]() ,
,![]() 进行“倍移”操作得到的点分别为
进行“倍移”操作得到的点分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)当![]() ,
,![]() 时,
时,
①若点![]() 表示的数为
表示的数为![]() ,则它的对应点
,则它的对应点![]() 表示的数为 .若点
表示的数为 .若点![]() 表示的数是
表示的数是![]() ,则点
,则点![]() 表示的数为 ; ②数轴上的点
表示的数为 ; ②数轴上的点![]() 表示的数为1,若
表示的数为1,若![]() ,则点
,则点![]() 表示的数为 ;
表示的数为 ;
(2)当![]() 时,若点
时,若点![]() 表示的数为
表示的数为![]() ,则
,则![]() 的值为 ;
的值为 ;
(3)若线段![]() ,请写出你能由此得到的结论.
,请写出你能由此得到的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.以下说法错误的是
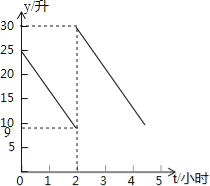
A.加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=﹣8t+25
B.途中加油21升
C.汽车加油后还可行驶4小时
D.汽车到达乙地时油箱中还余油6升
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民使用自来水,每户每月水费按如下标准收费:月用水量不超过8立方米,按每立方米a元收取;月用水量超过8立方米但不超过14立方米的部分,按每立方米b元收取;月用水量超过14立方米的部分,按每立方米c元收取.下表是某月部分居民的用水量及缴纳水费的数据.
用水量(立方米) | 2.5 | 15 | 6 | 12 | 10.3 | 4.7 | 9 | 17 | 16 |
水费(元) | 5 | 33.4 | 12 | 25.6 | 21.52 | 9.4 | 18.4 | 39.4 | 36.4 |
(1) ①a= _____,b= _____,c= _____;
②若小明家七月份需缴水费31元,则小明家七月份用水 米3;
(2) 该市某用户两个月共用水30立方米,设该用户在其中一个月用水x立方米,请列式表示这两个月该用户应缴纳的水费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,BC=6,D、E分别在BC、AC上,且DE∥AC,MN是△BDE的中位线.将线段DE从BD=2处开始向AC平移,当点D与点C重合时停止运动,则在运动过程中线段MN所扫过的区域面积为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号内:1,﹣5,|﹣![]() |,﹣12,0,﹣3.14,+1.99,﹣(﹣6),
|,﹣12,0,﹣3.14,+1.99,﹣(﹣6),![]() .
.
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)正整数集合:{ …}
(4)分数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题
阅读材料:
两个两位数相乘,如果这两个因数的十位数字相同,个位数字的和是10,该类乘法的速算方法是:将一个因数的十位数字与另一个因数的十位数字加1的和相乘,所得的积作为计算结果的前两位,将两个因数的个位数字之积作为计算结果的后两位(数位不足两位,用0补齐)。
比如![]() ,它们乘积的前两位是
,它们乘积的前两位是![]() ,它们乘积的后两位是
,它们乘积的后两位是![]() ,所以
,所以![]() ;
;
再如![]() ,它们乘积的前两位是
,它们乘积的前两位是![]() ,它们乘积的后两位是
,它们乘积的后两位是![]() ,所以
,所以![]() ;
;
又如![]() ,
,![]() ,不足两位,就将6写在百位:
,不足两位,就将6写在百位:![]() ,不足两位,就将9写在个位,十位上写0,所以
,不足两位,就将9写在个位,十位上写0,所以![]()
该速算方法可以用我们所学的整式乘法与分解因式的知识说明其合理性;
设其中一个因数的十位数字为![]() ,个位数字是
,个位数字是![]() ,(
,(![]() 、
、![]() 表示1~9的整数),则该数可表示为
表示1~9的整数),则该数可表示为![]() ,另一因数可表示为
,另一因数可表示为![]() .
.
两数相乘可得:
![]()
![]()
![]()
![]()
![]() .
.
(注:其中![]() 表示计算结果的前两位,
表示计算结果的前两位,![]() 表示计算结果的后两位。)
表示计算结果的后两位。)
问题:
两个两位数相乘,如果其中一个因数的十位数字与个位数字相同,另一因数的十位数字与个位数字之和是10.
如![]() 、
、![]() 、
、![]() 等.
等.
(1)探索该类乘法的速算方法,请以![]() 为例写出你的计算步骤;
为例写出你的计算步骤;
(2)设十位数字与个位数字相同的因数的十位数字是![]() ,则该数可以表示为___________.
,则该数可以表示为___________.
设另一个因数的十位数字是![]() ,则该数可以表示为___________.(
,则该数可以表示为___________.(![]() 、
、![]() 表示1~9的正整数)
表示1~9的正整数)
(3)请针对问题(1)(2)中的计算,模仿阅读材料中所用的方法写出如:![]() 的运算式:____________________
的运算式:____________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com