
【题目】如图,在△ABC中,BD平分∠ABC,∠A=2∠C.
(1)若∠C=38°,则∠ABD= ;
(2)求证:BC=AB+AD;
(3)求证:BC2=AB2+ABAC.

【答案】(1)33°;(2)证明见解析.(3)证明见解析.
【解析】试题分析:(1)在BC上截取BE=AB,利用“边角边”证明△ABD和△BED全等,根据全等三角形对应边相等可得DE=AD,全等三角形对应角相等可得∠AED=∠A,然后求出∠C=∠CDE,根据等角对等边可得CE=DE,然后结合图形整理即可得证;
(2)由(1)知:△ABD≌△BED,根据全等三角形对应边相等可得DE=AD,全等三角形对应角相等可得∠AED=∠A,然后求出∠C=∠CDE,根据等角对等边可得CE=DE,等量代换得到EC=AD,即得答案BC=BE+EC=AB+AD;
(3)为了把∠A=2∠C转化成两个角相等的条件,可以构造辅助线:在AC上取BF=BA,连接AE,根据线段的垂直平分线的性质以及三角形的内角和定理的推论能够证明AB=F.再根据勾股定理表示出BC2,AB2.再运用代数中的公式进行计算就可证明.
试题解析:(1)在BC上截取BE=BA,如图1,
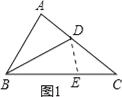
在△ABD和△BED中,
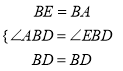 ,
,
∴△ABD≌△BED,
∴∠BED=∠A,
∵∠C=38°,∠A=2∠C,
∴∠A=76°,
∴∠ABC=180°﹣∠C﹣∠A=66°,
BD平分∠ABC,
∴∠ABD=33°;
(2)由(1)知:△ABD≌△BED,
∴BE=AB,DE=AD,∠BED=∠A,
又∵∠A=2∠C,
∴∠BED=∠C+∠EDC=2∠C,
∴∠EDC=∠C,
∴ED=EC,
∴EC=AD
∴BC=BE+EC=AB+AD;t
(3)如图2,过B作BG⊥AC于G,
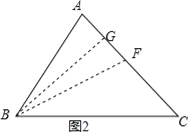
以B为圆心,BA长为半径画弧,交AC于F,
则BF=BA,
在Rt△ABG和Rt△GBG中,
![]() ,
,
∴Rt△ABG≌Rt△GBG,
∴AG=FG,
∴∠BFA=∠A,
∵∠A=2∠C,
∴∠BFA=∠FBC+∠C=2∠C,
∴∠FBC=∠C,
∴FB=FC,
FC=AB,
在Rt△ABG和Rt△BCG中,
BC2=BG2+CG2,
AB2=BG2+AG2
∴BC2﹣AB2=CG2﹣AG2=(CG+AG)(CG﹣AG)
=AC(CG﹣GF)=ACFC
=ACAB.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形网格中每个小正方形边长都是1.
(1)画出△ABC关于直线1对称的图形△A1BlCl;
(2)在直线l上找一点P,使PB=PC;(要求在直线1上标出点P的位置)
(3)连接PA、PC,计算四边形PABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式:①2x=2;②x=y;③﹣3﹣3=﹣6;④x+3x;⑤x﹣1=2x﹣3中,一元一次方程有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用为0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】搬进新居后,小杰自己动手用彩塑纸做了一个如图所示的正方形的挂式小饰品ABCD,彩线BD.AN.CM将正方形ABCD分成六部分,其中M是AB的中点,N是BC的中点,AN与CM交于O点.已知正方形ABCD的面积为576cm2,则被分隔开的△CON的面积为( )

A. 96cm2 B. 48cm2 C. 24cm2 D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为4cm,E,F分别为边DC,BC上的点,BF=1cm,CE=2cm,BE,DF相交于点G,求四边形CEGF的面积.
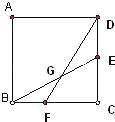
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com