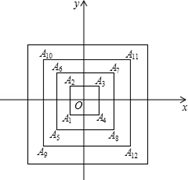
试题分析:(1)两者应该相等,由于四边形ADCB是矩形,那么对角线平分矩形的面积,同理OF也平分矩形AEFG的面积,由此就不难得出S
1=S
2了;
(2)S
3:S
2=1;3,也就能得出S
△AGF:S
△ADC=1:4,根据相似三角形的面积比等于相似比的平方,可得出OF:OC=1:2,即F为OC中点.由此可根据C、D的坐标直接求出F的坐标;
(3)由于A′F′始终在OC上,因此EE′所在的直线必平行于OC,可先求出直线EE′的解析式,然后根据E′横、纵坐标的比例关系来设出E′的坐标,代入直线EE′中即可求出E′A的坐标.
(1)S
1=S
2∵FE⊥y轴,FG⊥x轴,∠BAD=90°,
∴四边形AEFG是矩形.
∴AE=GF,EF=AG.
∴S
△AEF=S
△AFG,
同理S
△ABC=S
△ACD.
∴S
△ABC-S
△AEF=S
△ACD-S
△AFG.
即S
1=S
2.
(2)∵FG∥CD,
∴△AFG∽△ACD.
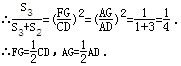
∵CD=BA=6,AD=BC=8,
∴FG=3,AG=4.
∴F(4,3);
(3)∵△A′E′F′是由△AEF沿直线AC平移得到的,且A′、F′两点始终在直线AC上,
∴点E′在过点E(0,3)且与直线AC平行的直线l上移动.
∵直线AC的解析式是y=
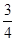
x,
∴直线L的解析式是y=
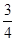
x+3.
设点E′为(x,y),
∵点E′到x轴的距离与到y轴的距离比是5:4,
∴|y|:|x|=5:4.

∴E′(6,7.5);
∴存在满足条件的E′坐标分别是( 6,
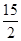
) (
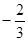
,
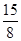
).
点评:此类问题难度较大,在中考中比较常见,一般在压轴题中出现,需特别注意.



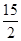 ) (
) (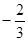 ,
,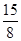 )
)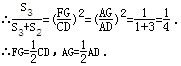
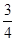 x,
x,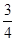 x+3.
x+3.
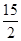 ) (
) (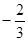 ,
,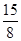 ).
).

 培优口算题卡系列答案
培优口算题卡系列答案 的位置,点B的横坐标为2,则点
的位置,点B的横坐标为2,则点 的坐标为
的坐标为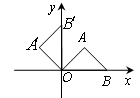
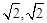 )
)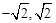 )
)