
 “―÷ΣΘ§»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§ΒψAΓΔBΓΔCΖ÷±πΈΣΉχ±ξ÷α…œΒΡ»ΐΗωΒψΘ§«“OA=1Θ§OB=3Θ§OC=4Θ°
“―÷ΣΘ§»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§ΒψAΓΔBΓΔCΖ÷±πΈΣΉχ±ξ÷α…œΒΡ»ΐΗωΒψΘ§«“OA=1Θ§OB=3Θ§OC=4Θ°Ζ÷Έω Θ®1Θ©ΗυΨί¥ΐΕ®œΒ ΐΖ®Θ§Ω…ΒΟΚ· ΐΫβΈω ΫΘ§ΗυΨί≈δΖΫΖ®Θ§Ω…ΒΟ¥πΑΗΘΜ
Θ®2Θ©ΗυΨί»¹»ǿΒΡ»ΐΫ«–ΈΟφΜΐœύΒ»Θ§Ω…ΒΟPΒψΒΡΉίΉχ±ξΘ§ΗυΨίΉ‘±δΝΩ”κΚ· ΐ÷ΒΒΡΕ‘”ΠΙΊœΒΘ§Ω…ΒΟ¥πΑΗΘΜ
Θ®3Θ©ΗυΨίΝβ–ΈΒΡΥΡ±ΏœύΒ»Θ§Ω…ΒΟQBΒΡ≥ΛΘ§ΗυΨίΝβ–ΈΒΡΕ‘±ΏΤΫ––Θ§Ω…ΒΟQΒψΒΡΉίΉχ±ξΘ°
Ϋβ¥π ΫβΘΚΘ®1Θ©…η≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=ax2+bx+cΘ§
ΓΏOA=1Θ§OB=3Θ§OC=4Θ°
ΓύAΘ®1Θ§0Θ©ΓΔBΘ®0Θ§3Θ©ΓΔCΘ®-4Θ§0Θ©Θ§
ΫΪAΘ§BΘ§C¥ζ»κΚ· ΐΫβΈω ΫΘ§ΒΟ
Γύ$\left\{\begin{array}{l}a+b+c=0\\ c=3\\ 16a-4b+c=0\end{array}\right.$
ΫβΒΟΘΚa=$-\frac{3}{4}$Θ§b=$-\frac{9}{4}$Θ§c=3Θ§
ΓύΨ≠ΙΐAΓΔBΓΔC»ΐΒψΒΡ≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=$-\frac{3}{4}$x2$-\frac{9}{4}$x+3ΘΜ
ΓΏy=$-\frac{3}{4}$x2$-\frac{9}{4}$x+3=$-\frac{3}{4}$Θ®x+$\frac{3}{2}$Θ©2+$\frac{75}{16}$
Γύ≈ΉΈοœΏΒΡΕΞΒψΉχ±ξ «Θ®$-\frac{3}{2}Θ§\frac{75}{16}$Θ©Θ§
Θ®2Θ©‘Ύ≈ΉΈοœΏ…œ¥φ‘Ύ“ΜΒψPΘ§ ΙΓςACPΒΡΟφΜΐΒ»”ΎΓςACBΒΡΟφΜΐΘ§άμ”…ΈΣΘΚ
…ηΒψPΒΡΉχ±ξΈΣPΘ®mΘ§nΘ©Θ§
ΓΏSΓςACB=$\frac{1}{2}$ΓΝ5ΓΝ3=$\frac{15}{2}$Θ§SΓςACP=$\frac{1}{2}$ΓΝ5ΓΝ|n|
Γύ$\frac{1}{2}$ΓΝ5ΓΝ|n|=$\frac{15}{2}$Θ§n=Γά3
ΓύΒ±n=3 ±Θ§$-\frac{3}{4}$x2$-\frac{9}{4}$x+3=3Θ§ΫβΒΟx1=0Θ®…αΘ©Θ§x2=-3Φ¥PΘ®-3Θ§3Θ©
Β±n=-3 ±Θ§$-\frac{3}{4}$x2$-\frac{9}{4}$x+3=-3Θ§ΫβΒΟx1=$\frac{{-3+\sqrt{41}}}{2}$Θ§x2=$\frac{{-3-\sqrt{41}}}{2}$Θ§Φ¥P 2Θ®$\frac{{-3+\sqrt{41}}}{2}$Θ§-3Θ©Θ§P3Θ®$\frac{{-3-\sqrt{41}}}{2}$Θ§-3Θ©
Ήέ…œΥυ ωΘΚPΒΡΉχ±ξΈΣP 1Θ®-3Θ§3Θ©Θ§P 2Θ®$\frac{{-3+\sqrt{41}}}{2}$Θ§-3Θ©Θ§P3Θ®$\frac{{-3-\sqrt{41}}}{2}$Θ§-3Θ©
Θ®3Θ©‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–¥φ‘Ύ“ΜΒψQΘ§ ΙΒΟ“‘ΒψAΓΔBΓΔCΓΔQΈΣΕΞΒψΒΡΥΡ±Ώ–ΈΈΣΝβ–ΈΘ§άμ”…ΈΣΘΚ
ΓΏOB=3Θ§OC=4Θ§OA=1Θ§
ΓύBC=AC=5Θ§
Β±BQΤΫ––«“Β»”ΎAC ±Θ§ΥΡ±Ώ–ΈACBPΈΣΝβ–ΈΘ§
ΓύBQ=AC=BC=5Θ§
ÿÿBQøACȧ
ΓύΒψQΒΫx÷αΒΡΨύάκΒ»”ΎOB=3Θ§
ΓύΒψQΒΡΉχ±ξΈΣΘ®5Θ§3Θ©Θ§
Β±ΒψQ‘ΎΒΎΕΰΓΔ»ΐœσœό ±Θ§“‘ΒψAΓΔBΓΔCΓΔQΈΣΕΞΒψΒΡΥΡ±Ώ–Έ÷ΜΡή «ΤΫ––ΥΡ±Ώ–ΈΘ§≤Μ «Νβ–ΈΘ§
‘ρΒ±ΒψQΒΡΉχ±ξΈΣΘ®5Θ§3Θ© ±Θ§“‘ΒψAΓΔBΓΔCΓΔQΈΣΕΞΒψΒΡΥΡ±Ώ–ΈΈΣΝβ–ΈΘ°
ΒψΤά ±ΨΧβΩΦ≤ιΝΥΕΰ¥ΈΚ· ΐΉέΚœΧβΘ§ΫβΘ®1Θ©ΒΡΙΊΦϋ «¥ΐΕ®œΒ ΐΖ®Θ§ΫβΘ®2Θ©ΒΡΙΊΦϋ «άϊ”Ο»¹»ǿΒΡ»ΐΫ«–ΈΟφΜΐœύΒ»ΒΟ≥ωPΒψΒΡΉίΉχ±ξΘ§”–άϊ”ΟΉ‘±δΝΩ”κΚ· ΐ÷ΒΒΡΕ‘”ΠΙΊœΒΘΜΫβΘ®3Θ©ΒΡΙΊΦϋ «άϊ”ΟΝβ–ΈΒΡΥΡ±ΏœύΒ»ΒΟ≥ωQBΒΡ≥ΛΘ°


 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
 “―÷Σ»γΆΦΘ§“Μ¥ΈΚ· ΐy=ax+bΚΆΖ¥±»άΐΚ· ΐy=$\frac{k}{x}$ΒΡΆΦœσœύΫΜ”ΎAΓΔBΝΫΒψΘ§≤ΜΒ» Ϋax+bΘΨ$\frac{k}{x}$ΒΡΫβΦ·ΈΣΘ®ΓΓΓΓΘ©
“―÷Σ»γΆΦΘ§“Μ¥ΈΚ· ΐy=ax+bΚΆΖ¥±»άΐΚ· ΐy=$\frac{k}{x}$ΒΡΆΦœσœύΫΜ”ΎAΓΔBΝΫΒψΘ§≤ΜΒ» Ϋax+bΘΨ$\frac{k}{x}$ΒΡΫβΦ·ΈΣΘ®ΓΓΓΓΘ©| AΘ° | xΘΦ-3 | BΘ° | xΘΦ-3ΜρxΘΨ1 | CΘ° | -3ΘΦxΘΦ0ΜρxΘΨ1 | DΘ° | -3ΘΦxΘΦ1 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $\frac{1}{2017}$ | BΘ° | 2017 | CΘ° | -2017 | DΘ° | -$\frac{1}{2017}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | a2+a2=2a4 | BΘ° | a10Γ¬a2=a5 | CΘ° | a3•a2=a5 | DΘ° | Θ®a+3Θ©2=a2+9 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
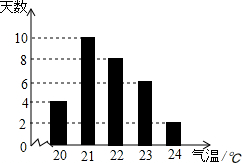 Ρ≥ –4‘¬ΖίΉνΗΏΤχΈ¬Ά≥ΦΤ»γΆΦΥυ ΨΘ§‘ρ‘ΎΉνΗΏΤχΈ¬’βΉι ΐΨί÷–Θ§÷Ύ ΐΚΆ÷–ΈΜ ΐΖ÷±π «Θ®ΓΓΓΓΘ©
Ρ≥ –4‘¬ΖίΉνΗΏΤχΈ¬Ά≥ΦΤ»γΆΦΥυ ΨΘ§‘ρ‘ΎΉνΗΏΤχΈ¬’βΉι ΐΨί÷–Θ§÷Ύ ΐΚΆ÷–ΈΜ ΐΖ÷±π «Θ®ΓΓΓΓΘ©| AΘ° | 21Θ§21 | BΘ° | 21Θ§21.5 | CΘ° | 21Θ§22 | DΘ° | 22Θ§22 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° |  | BΘ° |  | CΘ° |  | DΘ° |  |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° |  | BΘ° |  | CΘ° |  | DΘ° |  |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
 »γΆΦΘ§ΫΪ“ΜΩιΚ§”–30ΓψΫ«ΒΡ÷±Ϋ«»ΐΫ«ΑεΒΡΝΫΗωΕΞΒψΒΰΖ≈‘ΎΨΊ–ΈΒΡΝΫΧθΕ‘±Ώ…œΘ§»γΙϊΓœ1=ΠΝΕ»Θ§Γœ2=Π¬Ε»Θ§‘ρΘ®ΓΓΓΓΘ©
»γΆΦΘ§ΫΪ“ΜΩιΚ§”–30ΓψΫ«ΒΡ÷±Ϋ«»ΐΫ«ΑεΒΡΝΫΗωΕΞΒψΒΰΖ≈‘ΎΨΊ–ΈΒΡΝΫΧθΕ‘±Ώ…œΘ§»γΙϊΓœ1=ΠΝΕ»Θ§Γœ2=Π¬Ε»Θ§‘ρΘ®ΓΓΓΓΘ©| AΘ° | ΠΝ+Π¬=150 | BΘ° | ΠΝ+Π¬=90 | CΘ° | ΠΝ+Π¬=60 | DΘ° | Π¬-ΠΝ=30 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com