
【题目】在平面直角坐标系xOy中,抛物线M:y=ax2+bx+c(a≠0)经过A(﹣1,0),且顶点坐标为B(0,1).
(1)求抛物线M的函数表达式;
(2)设F(t,0)为x轴正半轴上一点,将抛物线M绕点F旋转180°得到抛物线M1.
①抛物线M1的顶点B1的坐标为 ;
②当抛物线M1与线段AB有公共点时,结合函数的图象,求t的取值范围.
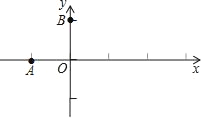
【答案】(1) y=-x2+1;(2)①(2t,-1);②0<t≤![]() .
.
【解析】
(1)利用顶点式列出函数表达式,再将另一个点的坐标代入函数表达式列出一元一次方程,求出函数表达式.
(2)作出图象,结合图象思考.
解:(1)∵抛物线的顶点坐标为B(0,1)
∴设抛物线M的函数表达式为y=ax2+1
∵抛物线M经过点A(-1,0)
∴a×(-1)2+1=0,解得a=-1
∴抛物线M的函数表达为y=-x2+1
(2) ①由题意得,点F为BB1的中点
∵F(t,0),设B1的坐标为(m,n)
∴![]() ,
,![]()
∴m=2t,n=-1
∴B1(2t,-1).
②由题意可知抛物线M1的顶点B1的坐标为(2t,-1),二次项系数为1,
∴抛物线M1的函数表达式为:y=(x-2t)2-1(t>0),
当抛物线M1经过点A(-1,0)时(如下图):
∴(-1-2t)2-1=0,解得t1=-1,t2=0;

当抛物线M1经过点B(0,1)时(如上图):
∴(0-2t)2-1=1,解得t=![]() .
.
结合图象分析,因为t>0,所以当抛物线M1与线段AB有公共点时,t的取值范围是0<t≤![]() .
.
故答案为:(1) y=-x2+1;(2)①(2t,-1);②0<t≤![]() .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为![]() 、宽为
、宽为![]() 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)
的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)

(1)观察图2请你写出![]() 、
、![]() 、
、![]() 之间的等量关系是______;
之间的等量关系是______;
(2)根据(1)中的结论,若![]() ,
,![]() ,则
,则![]() ______;
______;
(3)拓展应用:若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图16,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式.
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
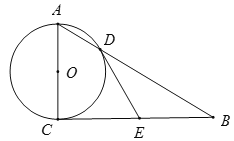
【题目】如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.
(1)直接写出ED和EC的数量关系:_________;
(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;
(3)填空:当BC=_______时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于一次函数y=﹣2x+3,下列结论正确的是( )
A. 图象过点(1,﹣1) B. 图象经过一、二、三象限
C. y随x的增大而增大 D. 当x>![]() 时,y<0
时,y<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com