
 如图,图中虚线部分使用围墙材料,其长度为70m,要使围成的矩形面积最大,长和宽分别为35m,35m.
如图,图中虚线部分使用围墙材料,其长度为70m,要使围成的矩形面积最大,长和宽分别为35m,35m. 科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
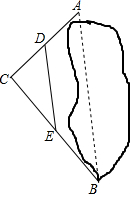 如图,要测定被池塘隔开的A,B两点的距离.可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接DE.现测得AC=30m,BC=40m,DE=24m,则AB=( )
如图,要测定被池塘隔开的A,B两点的距离.可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接DE.现测得AC=30m,BC=40m,DE=24m,则AB=( )| A. | 50m | B. | 48m | C. | 45m | D. | 35m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
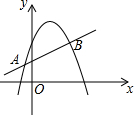 如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是x<-1或x>4.
如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是x<-1或x>4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
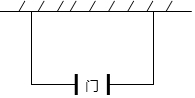 如图,某农场拟建一间饲养室,一面靠现有墙(墙足够长),且与现有墙相对的一侧墙体留有1m宽的门.已知计划中的材料可建墙体(不包括门)总长为11m,则能建成的饲养室总占地面积最大为( )m2.
如图,某农场拟建一间饲养室,一面靠现有墙(墙足够长),且与现有墙相对的一侧墙体留有1m宽的门.已知计划中的材料可建墙体(不包括门)总长为11m,则能建成的饲养室总占地面积最大为( )m2.| A. | 15 | B. | 16 | C. | 18 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
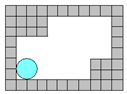 将半径为2cm的圆形纸板沿着挖空的部分方格纸板(小方格的边长为2cm)的内侧滚动一周,回到开始位置后,圆心经过的路线的长度为 ( )(精确到0.01cm)
将半径为2cm的圆形纸板沿着挖空的部分方格纸板(小方格的边长为2cm)的内侧滚动一周,回到开始位置后,圆心经过的路线的长度为 ( )(精确到0.01cm)| A. | 36cm | B. | 42.28cm | C. | 40.28cm | D. | 40cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com