
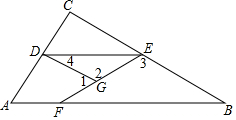
 已知:如图,△ABC中,点D、E分别是AC、BC上的一点,且∠1+∠3=180°,∠4=∠B.
已知:如图,△ABC中,点D、E分别是AC、BC上的一点,且∠1+∠3=180°,∠4=∠B. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
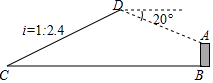 如图,已知点C与某建筑物底端B相距306米(点C与点B在同一水平面上),某同学从点C出发,沿同一剖面的斜坡CD行走195米至坡顶D处,斜坡CD的坡度(或坡比)i=1:2.4,在D处测得该建筑物顶端A的俯角为20°,则建筑物AB的高度约为(精确到0.1米,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)( )
如图,已知点C与某建筑物底端B相距306米(点C与点B在同一水平面上),某同学从点C出发,沿同一剖面的斜坡CD行走195米至坡顶D处,斜坡CD的坡度(或坡比)i=1:2.4,在D处测得该建筑物顶端A的俯角为20°,则建筑物AB的高度约为(精确到0.1米,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)( )| A. | 29.1米 | B. | 31.9米 | C. | 45.9米 | D. | 95.9米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某公司计划用32m长的材料沿墙建造的长方形仓库,仓库的一边靠墙,已知墙长16m,设长方形的宽AB为xm.
如图,某公司计划用32m长的材料沿墙建造的长方形仓库,仓库的一边靠墙,已知墙长16m,设长方形的宽AB为xm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
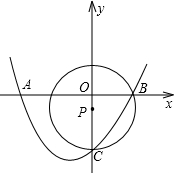 如图,抛物线y=ax2+bx+c(a≠0)经过x轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0,8),⊙P的圆心P在y轴上,且经过B、C两点,若b=2a,AB=6.
如图,抛物线y=ax2+bx+c(a≠0)经过x轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0,8),⊙P的圆心P在y轴上,且经过B、C两点,若b=2a,AB=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com